Mathematical discoveries from program search with large language models
- PMID: 38096900
- PMCID: PMC10794145
- DOI: 10.1038/s41586-023-06924-6
Mathematical discoveries from program search with large language models
Abstract
Large language models (LLMs) have demonstrated tremendous capabilities in solving complex tasks, from quantitative reasoning to understanding natural language. However, LLMs sometimes suffer from confabulations (or hallucinations), which can result in them making plausible but incorrect statements1,2. This hinders the use of current large models in scientific discovery. Here we introduce FunSearch (short for searching in the function space), an evolutionary procedure based on pairing a pretrained LLM with a systematic evaluator. We demonstrate the effectiveness of this approach to surpass the best-known results in important problems, pushing the boundary of existing LLM-based approaches3. Applying FunSearch to a central problem in extremal combinatorics-the cap set problem-we discover new constructions of large cap sets going beyond the best-known ones, both in finite dimensional and asymptotic cases. This shows that it is possible to make discoveries for established open problems using LLMs. We showcase the generality of FunSearch by applying it to an algorithmic problem, online bin packing, finding new heuristics that improve on widely used baselines. In contrast to most computer search approaches, FunSearch searches for programs that describe how to solve a problem, rather than what the solution is. Beyond being an effective and scalable strategy, discovered programs tend to be more interpretable than raw solutions, enabling feedback loops between domain experts and FunSearch, and the deployment of such programs in real-world applications.
© 2023. The Author(s).
Conflict of interest statement
The authors of the paper are planning to file a patent application relating to subject matter contained in this paper in the name of Google DeepMind.
Figures
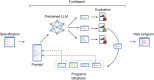

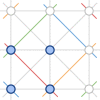






References
-
- Bang, Y. et al. A multitask, multilingual, multimodal evaluation of ChatGPT on reasoning, hallucination, and interactivity. Preprint at https://arxiv.org/abs/2302.04023 (2023).
-
- Borji, A. A. categorical archive of ChatGPT failures. Preprint at https://arxiv.org/abs/2302.03494 (2023).
-
- Lehman, J. et al. in Handbook of Evolutionary Machine Learning (eds Banzhaf, W. et al.) 331–366 (Springer, 2023).
-
- Chen, M. et al. Evaluating large language models trained on code. Preprint at https://arxiv.org/abs/2107.03374 (2021).
-
- Austin, J. et al. Program synthesis with large language models. Preprint at https://arxiv.org/abs/2108.07732 (2021).
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

