A computational toolbox for the assembly yield of complex and heterogeneous structures
- PMID: 38097568
- PMCID: PMC10721878
- DOI: 10.1038/s41467-023-43168-4
A computational toolbox for the assembly yield of complex and heterogeneous structures
Abstract
The self-assembly of complex structures from a set of non-identical building blocks is a hallmark of soft matter and biological systems, including protein complexes, colloidal clusters, and DNA-based assemblies. Predicting the dependence of the equilibrium assembly yield on the concentrations and interaction energies of building blocks is highly challenging, owing to the difficulty of computing the entropic contributions to the free energy of the many structures that compete with the ground state configuration. While these calculations yield well known results for spherically symmetric building blocks, they do not hold when the building blocks have internal rotational degrees of freedom. Here we present an approach for solving this problem that works with arbitrary building blocks, including proteins with known structure and complex colloidal building blocks. Our algorithm combines classical statistical mechanics with recently developed computational tools for automatic differentiation. Automatic differentiation allows efficient evaluation of equilibrium averages over configurations that would otherwise be intractable. We demonstrate the validity of our framework by comparison to molecular dynamics simulations of simple examples, and apply it to calculate the yield curves for known protein complexes and for the assembly of colloidal shells.
© 2023. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures
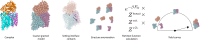
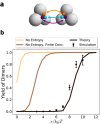
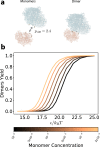


References
Grants and funding
- N00014-17- 1-3029/United States Department of Defense | United States Navy | Office of Naval Research (ONR)
- Investigator Award/Simons Foundation
- N00014-17- 1-3029,/United States Department of Defense | United States Navy | Office of Naval Research (ONR)
- N00014-17- 1-3029,/United States Department of Defense | United States Navy | Office of Naval Research (ONR)
- PHY-1734030/National Science Foundation (NSF)
LinkOut - more resources
Full Text Sources

