CoRegNet: unraveling gene co-regulation networks from public RNA-Seq repositories using a beta-binomial statistical model
- PMID: 38113079
- PMCID: PMC10729864
- DOI: 10.1093/bib/bbad380
CoRegNet: unraveling gene co-regulation networks from public RNA-Seq repositories using a beta-binomial statistical model
Abstract
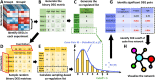
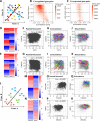
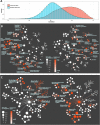
Millions of RNA sequencing samples have been deposited into public databases, providing a rich resource for biological research. These datasets encompass tens of thousands of experiments and offer comprehensive insights into human cellular regulation. However, a major challenge is how to integrate these experiments that acquired at different conditions. We propose a new statistical tool based on beta-binomial distributions that can construct robust gene co-regulation network (CoRegNet) across tens of thousands of experiments. Our analysis of over 12 000 experiments involving human tissues and cells shows that CoRegNet significantly outperforms existing gene co-expression-based methods. Although the majority of the genes are linearly co-regulated, we did discover an interesting set of genes that are non-linearly co-regulated; half of the time they change in the same direction and the other half they change in the opposite direction. Additionally, we identified a set of gene pairs that follows the Simpson's paradox. By utilizing public domain data, CoRegNet offers a powerful approach for identifying functionally related gene pairs, thereby revealing new biological insights.
Keywords: Simpson’s paradox; beta-binomial statistical model; co-regulation network; gene network; non-linear correlation.
© The Author(s) 2023. Published by Oxford University Press.
Figures