A kinetic model of iron trafficking in growing Saccharomyces cerevisiae cells; applying mathematical methods to minimize the problem of sparse data and generate viable autoregulatory mechanisms

Abstract

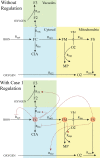
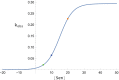
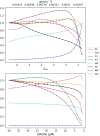
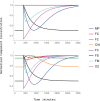
Iron is an essential transition metal for all eukaryotic cells, and its trafficking throughout the cell is highly regulated. However, the overall cellular mechanism of regulation is poorly understood despite knowing many of the molecular players involved. Here, an ordinary-differential-equations (ODE) based kinetic model of iron trafficking within a growing yeast cell was developed that included autoregulation. The 9-reaction 8-component in-silico cell model was solved under both steady-state and time-dependent dynamical conditions. The ODE for each component included a dilution term due to cell growth. Conserved rate relationships were obtained from the null space of the stoichiometric matrix, and the reduced-row-echelon-form was used to distinguish independent from dependent rates. Independent rates were determined from experimentally estimated component concentrations, cell growth rates, and the literature. Simple rate-law expressions were assumed, allowing rate-constants for each reaction to be estimated. Continuous Heaviside logistical functions were used to regulate rate-constants. These functions acted like valves, opening or closing depending on component "sensor" concentrations. Two cellular regulatory mechanisms were selected from 134,217,728 possibilities using a novel approach involving 6 mathematically-defined filters. Three cellular states were analyzed including healthy wild-type cells, iron-deficient wild-type cells, and a frataxin-deficient strain of cells characterizing the disease Friedreich's Ataxia. The model was stable toward limited perturbations, as determined by the eigenvalues of Jacobian matrices. Autoregulation allowed healthy cells to transition to the diseased state when triggered by a mutation in frataxin, and to the iron-deficient state when cells are placed in iron-deficient growth medium. The in-silico phenotypes observed during these transitions were similar to those observed experimentally. The model also predicted the observed effects of hypoxia on the diseased condition. A similar approach could be used to solve ODE-based kinetic models associated with other biochemical processes operating within growing cells.

Fig 1. The chemical model.

Top, without regulation; blue, yellow, and green regions represent cytosol, mitochondria, and vacuoles, respectively. Nutrient IRON enters the cytosol and becomes part of the labile iron pool (FC). Iron from this pool can either enter mitochondria, vacuole, or remain in the cytosol, converting to the CIA. This component was named after the Cytosolic Iron-sulfur Assembly protein complex, which functions to assemble iron-sulfur clusters in the cytosol. In this model, the CIA refers to all iron from FC that is not imported into mitochondria or vacuoles. Iron that enters vacuoles is stored, either as Fe^II (F2) or Fe^III (F3). Iron that enters mitochondria becomes part of another labile iron pool called FM which is used as substrate for the assembly of iron-sulfur clusters and hemes (FS). These centers are installed into, among other proteins, the respiratory complexes which ultimately reduce O2 to water. In healthy cells, this prevents O2 from penetrating into the mitochondrial matrix. However, in the diseased state, the “Respiratory shield” is weakened, and excessive O2 enters the matrix and reacts with FM to generate nanoparticles (MP) and reactive oxygen species (ROS). ROS is not shown as it is not included in the model (however, its rate of formation would be the same as MP). Names of reaction rates are indicated near the associated arrow. Bottom Panel: with regulation (CRM Case 1) shown in red dashed lines. Circles indicate sensed species. Feedback terms are indicated by perpendicular terminal lines. Feedforward terms are indicated by terminal arrows. According to this regulatory mechanism, there are three sensed species, including FC, FM, and FS. FC controls the rate of iron import into the cell, the rate of cytosolic iron import in vacuoles, and the oxidation of vacuolar Fe^II to Fe^III. FM controls the rate at which the cytosolic labile iron pool reacts to form the CIA, and the rate at which FM reactions with O2 to make nanoparticles. FS controls the rate by which cytosolic iron enters mitochondria and the rate by which nutrient OXYGEN enters the cell.

Fig 2. Behavior of continuous Heaviside Logistical functions in regulating rate-constants.

In this particular plot the ordinate is k₂₃ (as an example of a regulated k_obs) while the abscissa is [FC] (example of [Sen]). The solid blue line is the function calculated by nonlinear regression using parameters in Table 6. Orange, blue and green dots indicate k₂₃ for W, Y, and D states, respectively, as given in Table 3.

Fig 3. Normalized steady-state concentrations of model components during the transformation W → Y (top panel) and W → D (bottom panel).

The following plots represent the steady state transition for the 2 cases. CRM 1 is represented by a solid line while CRM 2 is the dotted line.

Fig 4. Normalized time-dependent concentrations of model components as the system transitions from W → Y and D → W (left side) and reverse (right side).

Left two panels: W → Y (top) and W → D (bottom); Right two panels: Y → W (top) and D → W (bottom).

Fig 5. Perturbation and recovery.

In this simulation, the system began in the W state with all components at their normalized steady-state concentrations except for [FS] which was normalized to 0.5. At t = 400 min, [FS] was doubled, and the system was allowed to recover in time. Top panel, without autoregulation; bottom panel, with Case 1 autoregulation.

Fig 6. Predicting the effect of hypoxia.

The system began in the W (left panel) and Y (right panel) states. At t = 0, the concentration of O2 was reduced from 100 μM to 25 μM (top) or to 1 μM (bottom). This caused the system to transition from W → H_W (top) and Y →H_Y (bottom).