Role of hierarchy structure on the mechanical adaptation of self-healing hydrogels under cyclic stretching

Abstract

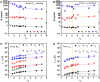
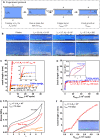
Soft materials with mechanical adaptability have substantial potential for various applications in tissue engineering. Gaining a deep understanding of the structural evolution and adaptation dynamics of soft materials subjected to cyclic stretching gives insight into developing mechanically adaptive materials. Here, we investigate the effect of hierarchy structure on the mechanical adaptation of self-healing hydrogels under cyclic stretching training. A polyampholyte hydrogel, composed of hierarchical structures including ionic bonds, transient and permanent polymer networks, and bicontinuous hard/soft-phase networks, is adopted as a model. Conditions for effective training, mild overtraining, and fatal overtraining are demonstrated in soft materials. We further reveal that mesoscale hard/soft-phase networks dominate the long-term memory effect of training and play a crucial role in the asymmetric dynamics of compliance changes and the symmetric dynamics of hydrogel shape evolution. Our findings provide insights into the design of hierarchical structures for adaptive soft materials.

Fig. 1.. Schematic illustrations of hierarchical structures in s-PA gel and their dynamic adaptation to mechanical training.

(A) Multiscale structure in s-PA gel, including ~1-nm transient network by dynamic ionic bonds, ~10-nm (mesh size ξ) permanent polymer network by entanglement and cross-linking, and ~100-nm (d-spacing d₀) bicontinuous hard/soft-phase networks by phase separation. The gel has at least three relaxation times related to the three networks (the transient network, the soft-phase network, and the hard-phase network). They are accumulations of ionic aggregations. (B) A scheme of the deformation of bicontinuous phase networks and transient network to cyclic training at conditions (I) λ_tr < λ_affine and (II) λ_affine < λ_tr < λ_c. I: Both the hard- and soft-phase networks are intact. II: Damage occurs in the hard-phase network, while the soft-phase network remains intact. λ_affine and λ_c are maximum stretch ratio for the onset for the damage of the hard- and soft-phase networks, respectively (fig. S1). (C) A scheme of effective training (Training I), overtraining (Training II), and detraining. Under successive cyclic training stimuli, a stretch-induced decrease of stiffness and strain energy to a specific deformation (W_d) that increased compliance of the material (red curve). For Training I, the stiffness and W_d recover during detraining (dashed green curves). The recovery rate depends on duration (t_tr) and training intensity. Overtraining occurred during Training II causing unrecoverable damage.

Fig. 2.. Cyclic training of s-PA gel and evolution of the bicontinuous phase structure.

(A) Experimental protocol for cyclic training and detraining (rest). L₀ = 50 mm, H₀ = 10 mm, and λ_tr = 1.7 to 7.1. (B) Evolution of loading-unloading curves with training cycle (N_tr). (C) Loading-unloading curves for a trained gel resting for t_rest. Training at λ_tr = 3.7 for N_tr = 10⁴ cycles is taken as an example. (D) Scheme for work of extension (W_ex, total hatched area) and the residual stretch ratio (λ_res). (E) Normalized W_ex/W_ex0 and λ_res in cyclic training and detraining as a function of time. Dashed arrows indicate the start point of detraining. The top scheme shows the corresponding training and detraining processes. Training at λ_tr = 3.7 for N_tr = 10⁴ is taken as an example. (F and G) Cyclic training-induced evolution of 2D SAXS patterns (F) and the corresponding 1D azimuthal scan profiles (G). The right inset in (G) shows the azimuthal scan’s integration q range (between two concentric circles). The left inset shows the evolution of full peak width at half maximum (ΔΨ_1/2) of unloading sample (strain-free state) as a function of training cycle N_tr. λ_tr = 2.9 < λ_affine is taken as an example. (H) Microscopic deformation (d_⊥/d₀) in perpendicular to loading direction versus macroscopic stretch ratio λ for loading to different cycle number N_tr at λ_tr = 3.44. The d_⊥/d₀ decreases with λ, due to lateral contraction of phase network when elongation along the stretch direction (51). The blue line stands for the prediction of affine deformation (d_⊥/d₀ = λ^−1/2) of the phase networks perpendicular to the loading direction (incompressible materials). The black arrow indicates the maximum λ to show affine deformation of the bicontinuous hard/soft-phase networks (λ_affine ≈ 3.06).

Fig. 3.. Characteristic training cycles and detraining times of s-PA gel at varied λ_tr for N_tr = 10⁴cycles.

Characteristic training cycles and characteristic detraining times were obtained from the three-term Prony series fitting (see the Supplementary Materials). (A and B) Characteristic training cycles N₁, N₂, and N₃ of W_ex (A) and λ_res (B) as a function of λ_tr. (C and D) Characteristic training time τ_i and characteristic detraining time τ_f,i versus λ_tr for W_ex (C) and λ_res (D). The vertical dashed line indicates λ_affine. Dashed lines are guides for the eyes. The error bar (λ_tr = 2.1 to 3.7) is SE from at least three measurements.

Fig. 4.. Role of training intensity (λ_tr), training duration (N_tr), and rest time (t_rest) on fatigue resistance of s-PA gel.

(A) Experimental protocol. The unnotched sample was trained at stretching ratio λ_tr for N_tr cycles, then allowed to rest for time t_rest, after which the sample was notched (c₀ = 10 mm), and then immediately subjected to fatigue testing at λ_fatigue = 2.9 for N_fatigue cycles to observe crack resistance. Crack growth length is denoted as c. (B and C) Typical crack tip shape (B) and fatigue crack propagation behavior (C) for samples trained at λ_tr = 2.9 for N_tr = 2000 and λ_tr = 3.7 for N_tr = 2000 and 200 with t_rest = 0. Inset is a zoom-in view of the initial 6000 cycles. (D) Fatigue results for the sample experienced mild overtraining (λ_tr = 3.7 for N_tr = 2000) and resting for t_rest = 55 hours. Inset shows the loading-unloading curve of the rested sample compared to the pristine sample. (E and F) Loading-unloading curves for gel trained at λ_tr = 7.1 for N_tr = 10⁴ and allowed to rest for t_rest = 10 days (E), and its fatigue test result (F).