Tuning Potential Functions to Host-Guest Binding Data
- PMID: 38147689
- PMCID: PMC10838530
- DOI: 10.1021/acs.jctc.3c01050
Tuning Potential Functions to Host-Guest Binding Data
Abstract
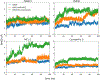
Software to more rapidly and accurately predict protein-ligand binding affinities is of high interest for early-stage drug discovery, and physics-based methods are among the most widely used technologies for this purpose. The accuracy of these methods depends critically on the accuracy of the potential functions that they use. Potential functions are typically trained against a combination of quantum chemical and experimental data. However, although binding affinities are among the most important quantities to predict, experimental binding affinities have not to date been integrated into the experimental data set used to train potential functions. In recent years, the use of host-guest complexes as simple and tractable models of binding thermodynamics has gained popularity due to their small size and simplicity, relative to protein-ligand systems. Host-guest complexes can also avoid ambiguities that arise in protein-ligand systems such as uncertain protonation states. Thus, experimental host-guest binding data are an appealing additional data type to integrate into the experimental data set used to optimize potential functions. Here, we report the extension of the Open Force Field Evaluator framework to enable the systematic calculation of host-guest binding free energies and their gradients with respect to force field parameters, coupled with the curation of 126 host-guest complexes with available experimental binding free energies. As an initial application of this novel infrastructure, we optimized generalized Born (GB) cavity radii for the OBC2 GB implicit solvent model against experimental data for 36 host-guest systems. This refitting led to a dramatic improvement in accuracy for both the training set and a separate test set with 90 additional host-guest systems. The optimized radii also showed encouraging transferability from host-guest systems to 59 protein-ligand systems. However, the new radii are significantly smaller than the baseline radii and lead to excessively favorable hydration free energies (HFEs). Thus, users of the OBC2 GB model currently may choose between GB cavity radii that yield more accurate binding affinities and GB cavity radii that yield more accurate HFEs. We suspect that achieving good accuracy on both will require more far-reaching adjustments to the GB model. We note that binding free-energy calculations using the OBC2 model in OpenMM gain about a 10× speedup relative to corresponding explicit solvent calculations, suggesting a future role for implicit solvent absolute binding free-energy (ABFE) calculations in virtual compound screening. This study proves the principle of using host-guest systems to train potential functions that are transferrable to protein-ligand systems and provides an infrastructure that enables a range of applications.
Figures
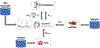

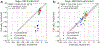
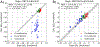


Similar articles
-
Binding Thermodynamics of Host-Guest Systems with SMIRNOFF99Frosst 1.0.5 from the Open Force Field Initiative.J Chem Theory Comput. 2019 Nov 12;15(11):6225-6242. doi: 10.1021/acs.jctc.9b00748. Epub 2019 Oct 25. J Chem Theory Comput. 2019. PMID: 31603667 Free PMC article.
-
Accuracy comparison of several common implicit solvent models and their implementations in the context of protein-ligand binding.J Mol Graph Model. 2017 Mar;72:70-80. doi: 10.1016/j.jmgm.2016.12.011. Epub 2016 Dec 21. J Mol Graph Model. 2017. PMID: 28064081 Free PMC article.
-
Overview of the SAMPL5 host-guest challenge: Are we doing better?J Comput Aided Mol Des. 2017 Jan;31(1):1-19. doi: 10.1007/s10822-016-9974-4. Epub 2016 Sep 22. J Comput Aided Mol Des. 2017. PMID: 27658802 Free PMC article. Review.
-
Evaluation of Generalized Born Models for Large Scale Affinity Prediction of Cyclodextrin Host-Guest Complexes.J Chem Inf Model. 2016 Oct 24;56(10):2080-2092. doi: 10.1021/acs.jcim.6b00418. Epub 2016 Oct 4. J Chem Inf Model. 2016. PMID: 27626790
-
The SAMPL4 host-guest blind prediction challenge: an overview.J Comput Aided Mol Des. 2014 Apr;28(4):305-17. doi: 10.1007/s10822-014-9735-1. Epub 2014 Mar 6. J Comput Aided Mol Des. 2014. PMID: 24599514 Free PMC article. Review.
Cited by
-
The Open Force Field Initiative: Open Software and Open Science for Molecular Modeling.J Phys Chem B. 2024 Jul 25;128(29):7043-7067. doi: 10.1021/acs.jpcb.4c01558. Epub 2024 Jul 11. J Phys Chem B. 2024. PMID: 38989715 Free PMC article.
-
BAT2: an Open-Source Tool for Flexible, Automated, and Low Cost Absolute Binding Free Energy Calculations.J Chem Theory Comput. 2024 Aug 13;20(15):6518-6530. doi: 10.1021/acs.jctc.4c00205. Epub 2024 Aug 1. J Chem Theory Comput. 2024. PMID: 39088306 Free PMC article.
-
Machine-learned molecular mechanics force fields from large-scale quantum chemical data.Chem Sci. 2024 Jun 26;15(32):12861-12878. doi: 10.1039/d4sc00690a. eCollection 2024 Aug 14. Chem Sci. 2024. PMID: 39148808 Free PMC article.
-
Optimal Dielectric Boundary for Binding Free Energy Estimates in the Implicit Solvent.J Chem Inf Model. 2024 Dec 23;64(24):9433-9448. doi: 10.1021/acs.jcim.4c01190. Epub 2024 Dec 10. J Chem Inf Model. 2024. PMID: 39656550 Free PMC article.
-
Reversible molecular simulation for training classical and machine-learning force fields.Proc Natl Acad Sci U S A. 2025 Jun 3;122(22):e2426058122. doi: 10.1073/pnas.2426058122. Epub 2025 May 28. Proc Natl Acad Sci U S A. 2025. PMID: 40434635 Free PMC article.
References
-
- Boresch S; Tettinger F; Leitgeb M; Karplus M Absolute Binding Free Energies: A Quantitative Approach for their Calculation. Journal of Physical Chemistry B 2003, 107, 9535–9551.
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
