What can entropy metrics tell us about the characteristics of ocular fixation trajectories?
- PMID: 38166054
- PMCID: PMC10760742
- DOI: 10.1371/journal.pone.0291823
What can entropy metrics tell us about the characteristics of ocular fixation trajectories?
Abstract
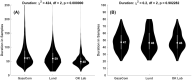
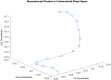
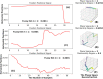
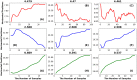
In this study, we provide a detailed analysis of entropy measures calculated for fixation eye movement trajectories from the three different datasets. We employed six key metrics (Fuzzy, Increment, Sample, Gridded Distribution, Phase, and Spectral Entropies). We calculate these six metrics on three sets of fixations: (1) fixations from the GazeCom dataset, (2) fixations from what we refer to as the "Lund" dataset, and (3) fixations from our own research laboratory ("OK Lab" dataset). For each entropy measure, for each dataset, we closely examined the 36 fixations with the highest entropy and the 36 fixations with the lowest entropy. From this, it was clear that the nature of the information from our entropy metrics depended on which dataset was evaluated. These entropy metrics found various types of misclassified fixations in the GazeCom dataset. Two entropy metrics also detected fixation with substantial linear drift. For the Lund dataset, the only finding was that low spectral entropy was associated with what we call "bumpy" fixations. These are fixations with low-frequency oscillations. For the OK Lab dataset, three entropies found fixations with high-frequency noise which probably represent ocular microtremor. In this dataset, one entropy found fixations with linear drift. The between-dataset results are discussed in terms of the number of fixations in each dataset, the different eye movement stimuli employed, and the method of eye movement classification.
Copyright: © 2024 Melnyk et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
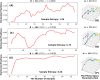
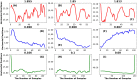



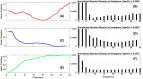
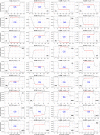
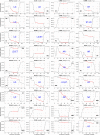

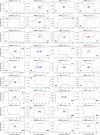
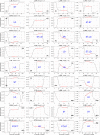





Similar articles
-
Gaze-in-wild: A dataset for studying eye and head coordination in everyday activities.Sci Rep. 2020 Feb 13;10(1):2539. doi: 10.1038/s41598-020-59251-5. Sci Rep. 2020. PMID: 32054884 Free PMC article.
-
Do people with Parkinson's disease look at task relevant stimuli when walking? An exploration of eye movements.Behav Brain Res. 2018 Aug 1;348:82-89. doi: 10.1016/j.bbr.2018.03.003. Epub 2018 Mar 17. Behav Brain Res. 2018. PMID: 29559336
-
The origin of ocular microtremor in man.Exp Brain Res. 1999 Jun;126(4):556-62. doi: 10.1007/s002210050764. Exp Brain Res. 1999. PMID: 10422719
-
I'm not sure that curve means what you think it means: Toward a [more] realistic understanding of the role of eye-movement generation in the Visual World Paradigm.Psychon Bull Rev. 2023 Feb;30(1):102-146. doi: 10.3758/s13423-022-02143-8. Epub 2022 Aug 12. Psychon Bull Rev. 2023. PMID: 35962241 Free PMC article. Review.
-
Predicting Visual Fixations.Annu Rev Vis Sci. 2023 Sep 15;9:269-291. doi: 10.1146/annurev-vision-120822-072528. Epub 2023 Jul 7. Annu Rev Vis Sci. 2023. PMID: 37419107 Review.
References
-
- Lohr D, Berndt SH, Komogortsev O. An Implementation of Eye Movement-Driven Biometrics in Virtual Reality. In: Proceedings of the 2018 ACM Symposium on Eye Tracking Research & Applications. ETRA’18. New York, NY, USA: Association for Computing Machinery; 2018. p. 1–3. Available from: 10.1145/3204493.3208333. - DOI
-
- Griffith HK, Komogortsev OV. Texture Feature Extraction From Free-Viewing Scan Paths Using Gabor Filters With Downsampling. In: ACM Symposium on Eye Tracking Research and Applications. ETRA’20 Adjunct. New York, NY, USA: Association for Computing Machinery; 2020. p. 1–3. Available from: 10.1145/3379157.3391423. - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous

