DomiRank Centrality reveals structural fragility of complex networks via node dominance

Abstract

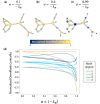
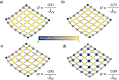
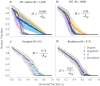
Determining the key elements of interconnected infrastructure and complex systems is paramount to ensure system functionality and integrity. This work quantifies the dominance of the networks' nodes in their respective neighborhoods, introducing a centrality metric, DomiRank, that integrates local and global topological information via a tunable parameter. We present an analytical formula and an efficient parallelizable algorithm for DomiRank centrality, making it applicable to massive networks. From the networks' structure and function perspective, nodes with high values of DomiRank highlight fragile neighborhoods whose integrity and functionality are highly dependent on those dominant nodes. Underscoring this relation between dominance and fragility, we show that DomiRank systematically outperforms other centrality metrics in generating targeted attacks that effectively compromise network structure and disrupt its functionality for synthetic and real-world topologies. Moreover, we show that DomiRank-based attacks inflict more enduring damage in the network, hindering its ability to rebound and, thus, impairing system resilience. DomiRank centrality capitalizes on the competition mechanism embedded in its definition to expose the fragility of networks, paving the way to design strategies to mitigate vulnerability and enhance the resilience of critical infrastructures.

Fig. 1. Computational cost of DomiRank.

Mean (30 samples) computational costs to compute DomiRank analytically and estimate it recursively on a multi-threaded CPU and on the GPU as a function of the network size N. The mean DomiRank computational cost is also compared with the mean computational cost for estimating PageRank on the same multi-threaded CPU and GPU. The convergence criterion is evaluated using the L1 error between two consecutive iterations - i.e., $\frac{1}{N}\mid \mid \mathit{\Gamma }\left(t\right)-\mathit{\Gamma }\left(t+dt\right)\mid {\mid }_1<dt\cdot ϵ$, with a threshold set to ϵ = 10⁻⁶ (note that for the chosen convergence threshold, the Spearman correlation with the analytical solution is > 0.9999999).

Fig. 2. DomiRank for different levels of competition (σ).

DomiRank centrality is displayed on the nodes of a simple network with N = 15 nodes for a low, b medium, and c large values of σ. Panel d shows the DomiRank centrality as a function of σ, wherein each solid line represents a specific node (color encoding node degree). In panels a–c, the direction of the pairwise transfer of fitness between nodes is shown by arrows, with their thickness representing the magnitude of that exchange. Note that for visualization purposes, the arrow thickness in panels a–c are scaled 25: 5: 1.

Fig. 3. The role of σ in setting DomiRank values.

DomiRank centrality is displayed on the nodes of a 2D-square lattice with N = 49 nodes for different values of σ a $\frac{0.01}{-{\lambda }_N}$, b $\frac{0.75}{-{\lambda }_N}$, c $\frac{0.95}{-{\lambda }_N}$ and d $\frac{0.99}{-{\lambda }_N}$ to illustrate different levels of competition, and how those levels set the trade-off between local (nodal) and global (meso- to large- scale structure) network information conveyed by DomiRank. Note that for each panel, the values of DomiRank are normalized to range in interval [0, 1] for enhanced visualization.

Fig. 4. Comparing DomiRank with other centralities in dismantling toy networks.

Evolution of the relative size of the largest connected component whilst undergoing sequential node removal according to descending scores of various centralities for three toy networks: a 2D regular lattice (N = 49), e Erdős-Rényi (ER; N = 32), and i Barabási-Albert (BA; N = 25). For each topology, panels b–d, f–h, and j–l show the graphical representation of the respective networks at various stages of the attack based on DomiRank, betweenness, closeness, and PageRank centralities. Note that the nodes are colored according to the relative value of the centralities normalized to be in an interval [0, 1] for enhancing comparability and visualization purposes.

Fig. 5. Centrality-based attacks on synthetic and real-world networks.

Evolution of the relative size of the largest connected component (robustness) whilst undergoing sequential node removal according to descending scores of various centrality measures for different synthetic networks of size N = 1000: a Watts-Strogratz (WS; small-world, $\overline{k}=4$), Erdős-Rényi (ER) with b high ($\overline{k}=20$) and e low link density ($\overline{k}=6$), c random geometric graph (RGG; $\overline{k}=16$), d stochastic block model (SBM; $\overline{k}=7$), and f Barabási-Albert (BA; $\overline{k}=6$). The performance of the attacks based on the different centrality metrics is also shown for different real networks: g hub-dominated transport network (airline connections, $\overline{k}=16$), h neural network (worm, $\overline{k}=29$), i spatial network (power-grid, $\overline{k}=3$), j citation network ($\overline{k}=25$), k massive social network ($\overline{k}=19$), and l massive spatial transport network (roads, $\overline{k}=5$). Note that for panels j–l, where massive networks are shown, only a few attack strategies are displayed due to the impossibility of computation of the rest.

Fig. 6. Assessing the effect of iterative centrality-based attacks and recovery mechanisms on network resilience.

Panels a–d show the evolution of the relative size of the largest connected component of various synthetic networks of size N = 500, namely; a Watts-Strogatz (WS; $\overline{k}=4$), b Barabási-Albert (BA; $\overline{k}=4$), c Erdős-Rényi (ER; $\overline{k}=4$), and d random geometric graph (RGG; $\overline{k}=7$), undergoing sequential node removal based on iteratively computed centralities and on pre-computed DomiRank. Panels e–h show the evolution of the relative size of the largest connected component for the same networks undergoing sequential node removal based on pre-computed DomiRank (optimal and high σ), iterative betweenness, and Collective Influence (CI), where a stochastic first-in-first-out node recovery (stack recovery implementation) process, with a probability of recovery p = 0.25 per time step, is implemented.

Fig. 7. Functional robustness of synthetic and real-world networks under centrality-based attacks.

Average rumor spread fraction (error-bars representing the standard deviation) of 1000 rumor spreading simulations as a function of the subsequent network stage resulting of sequential node removal according to degree, PageRank, DomiRank, and Collective Influence strategies, for two synthetic networks: a 2D regular lattice ($\overline{k}=4$) and b Watts-Strogatz (WS; $\overline{k}=6$), and two real networks: c a contact-tracing social network (Hospital; $\overline{k}=30$) and d a survey based social network (Residence; $\overline{k}=16$).