Fractional quantum ferroelectricity

Abstract

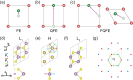
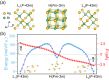
For an ordinary ferroelectric, the magnitude of the spontaneous electric polarization is at least one order of magnitude smaller than that resulting from the ionic displacement of the lattice vectors, and the direction of the spontaneous electric polarization is determined by the point group of the ferroelectric. Here, we introduce a new class of ferroelectricity termed Fractional Quantum Ferroelectricity. Unlike ordinary ferroelectrics, the polarization of Fractional Quantum Ferroelectricity arises from substantial atomic displacements that are comparable to lattice constants. Applying group theory analysis, we identify 28 potential point groups that can realize Fractional Quantum Ferroelectricity, including both polar and non-polar groups. The direction of polarization in Fractional Quantum Ferroelectricity is found to always contradict with the symmetry of the "polar" phase, which violates Neumann's principle, challenging conventional symmetry-based knowledge. Through the Fractional Quantum Ferroelectricity theory and density functional calculations, we not only explain the puzzling experimentally observed in-plane polarization of monolayer α-In₂Se₃, but also predict polarization in a cubic compound of AgBr. Our findings unveil a new realm of ferroelectric behavior, expanding the understanding and application of these materials beyond the limits of traditional ferroelectrics.

Fig. 1. Concept of FQFE.

Schematics of a FE, b QFE and c FQFE, supposing the ion with ±1 charges. The green and red balls represent movable ions and ligand ions, respectively. Top and side views of the FQFE example: d low-symmetry phase L₁, e high-symmetry phase H, f low-symmetry phase L₂. The black border indicates the unit cell. F includes two are fixed atoms (layers) F, and M is a movable atom (layer). The blue and red arrows depict the atomic displacements of M from H to L₁ and L₂, respectively. The green arrows show ∆P, the atomic displacements of M between L₁ and L₂. Since only M moves, the blue, red, and green arrows can also represent P₁(polarization of L₁), P₂(polarization of L₂), and ∆P (polarization difference between low symmetry phases), respectively. ∆P cannot be invariant under a point symmetry operation (C_3z) of the low-symmetry phase, which leads to the FQFE. g The latticed form of P₁, P₂ and ∆P. The black dashed parallelogram depicts the “lattice” of polarization. The blue and red points represent P₁ and P₂, respectively. ∆P can be any vector between points with different color. Therefore, ∆P is non-zero and fractionally quantized, i.e. $\frac{1}{3}\mathbf{Q}$ along the [120] direction.

Fig. 2. Structure and ferroelectricity of monolayer α-In₂Se₃.

a Top and side views of monolayer α-In₂Se₃, corresponding to the L₁, H, and L₂ phases, respectively. $\frac{1}{3}\mathbf{a}+\frac{1}{3}\mathbf{b}$, the in-plane displacement of M (Se) in the ferroelectric phase transition is shown by the blue arrow. b NEB calculation of the energy barrier and evolution of the polarization intensity along the path similar to the one in Ref. . The amplitude represents the in-plane polarization magnitude along the [110] direction. The positive and negative signs indicate the polarization toward [110] and the [−1–10] direction, respectively. Here the polarizations of L₁ and L₂ are ${\mathbf{P}}_1=\frac{1}{3}\mathbf{Q}$ and ${\mathbf{P}}_2=-\frac{1}{3}\mathbf{Q}$, respectively. Q is the polarization quantum along the [110] direction. The polarization difference is $\mathit{△}\mathbf{P}=\frac{2}{3}\mathbf{Q}$.

Fig. 3. Structure and ferroelectricity of bulk AgBr.

a Schematic structure of AgBr during the L₁-H-L₂ phase transition. The L_1,2 phase belongs to F-43m and the H phase belongs to Fm-3m. The process can be considered as Br moving along the path $\left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)\to \left(\frac{1}{2},\frac{1}{2},\frac{1}{2}\right)\to \left(\frac{3}{4},\frac{3}{4},\frac{3}{4}\right)$. b The energy barrier calculated by NEB and the evolution of the polarization in the primitive cell along the path in (a), where the primitive cells of L₁, H, L₂ are depicted. Here the polarizations of L₁ and L₂ are ${\mathbf{P}}_1=\frac{1}{4}\mathbf{Q}$ and ${\mathbf{P}}_2=-\frac{1}{4}\mathbf{Q}$, respectively. Q is the polarization quantum along the [111] direction. The polarization difference is $\mathit{△}\mathbf{P}=\frac{1}{2}\mathbf{Q}$.