Generalized Shape Metrics on Neural Representations
- PMID: 38170102
- PMCID: PMC10760997
Generalized Shape Metrics on Neural Representations
Abstract
Understanding the operation of biological and artificial networks remains a difficult and important challenge. To identify general principles, researchers are increasingly interested in surveying large collections of networks that are trained on, or biologically adapted to, similar tasks. A standardized set of analysis tools is now needed to identify how network-level covariates-such as architecture, anatomical brain region, and model organism-impact neural representations (hidden layer activations). Here, we provide a rigorous foundation for these analyses by defining a broad family of metric spaces that quantify representational dissimilarity. Using this framework, we modify existing representational similarity measures based on canonical correlation analysis and centered kernel alignment to satisfy the triangle inequality, formulate a novel metric that respects the inductive biases in convolutional layers, and identify approximate Euclidean embeddings that enable network representations to be incorporated into essentially any off-the-shelf machine learning method. We demonstrate these methods on large-scale datasets from biology (Allen Institute Brain Observatory) and deep learning (NAS-Bench-101). In doing so, we identify relationships between neural representations that are interpretable in terms of anatomical features and model performance.
Figures



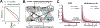
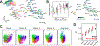
References
-
- Barrett David GT, Morcos Ari S, and Macke Jakob H. “Analyzing biological and artificial neural networks: challenges with opportunities for synergy?” Current Opinion in Neurobiology 55 (2019). Machine Learning, Big Data, and Neuroscience, pp. 55–64. - PubMed
-
- Kriegeskorte Nikolaus and Wei Xue-Xin. “Neural tuning and representational geometry”. Nature Reviews Neuroscience (2021). - PubMed
-
- Roeder Geoffrey, Metz Luke, and Kingma Durk. “On Linear Identifiability of Learned Representations”. Proceedings of the 38th International Conference on Machine Learning. Ed. by Meila Marina and Zhang Tong. Vol. 139. Proceedings of Machine Learning Research. PMLR, 2021, pp. 9030–9039.
-
- Cadena Santiago A., Sinz Fabian H., Muhammad Taliah, Froudarakis Emmanouil, Cobos Erick, Walker Edgar Y., Reimer Jake, Bethge Matthias, Tolias Andreas, and Ecker Alexander S.. “How well do deep neural networks trained on object recognition characterize the mouse visual system?” NeurIPS Workshop Neuro AI (2019).
Grants and funding
LinkOut - more resources
Full Text Sources
