Multifractality in spin glasses

Abstract

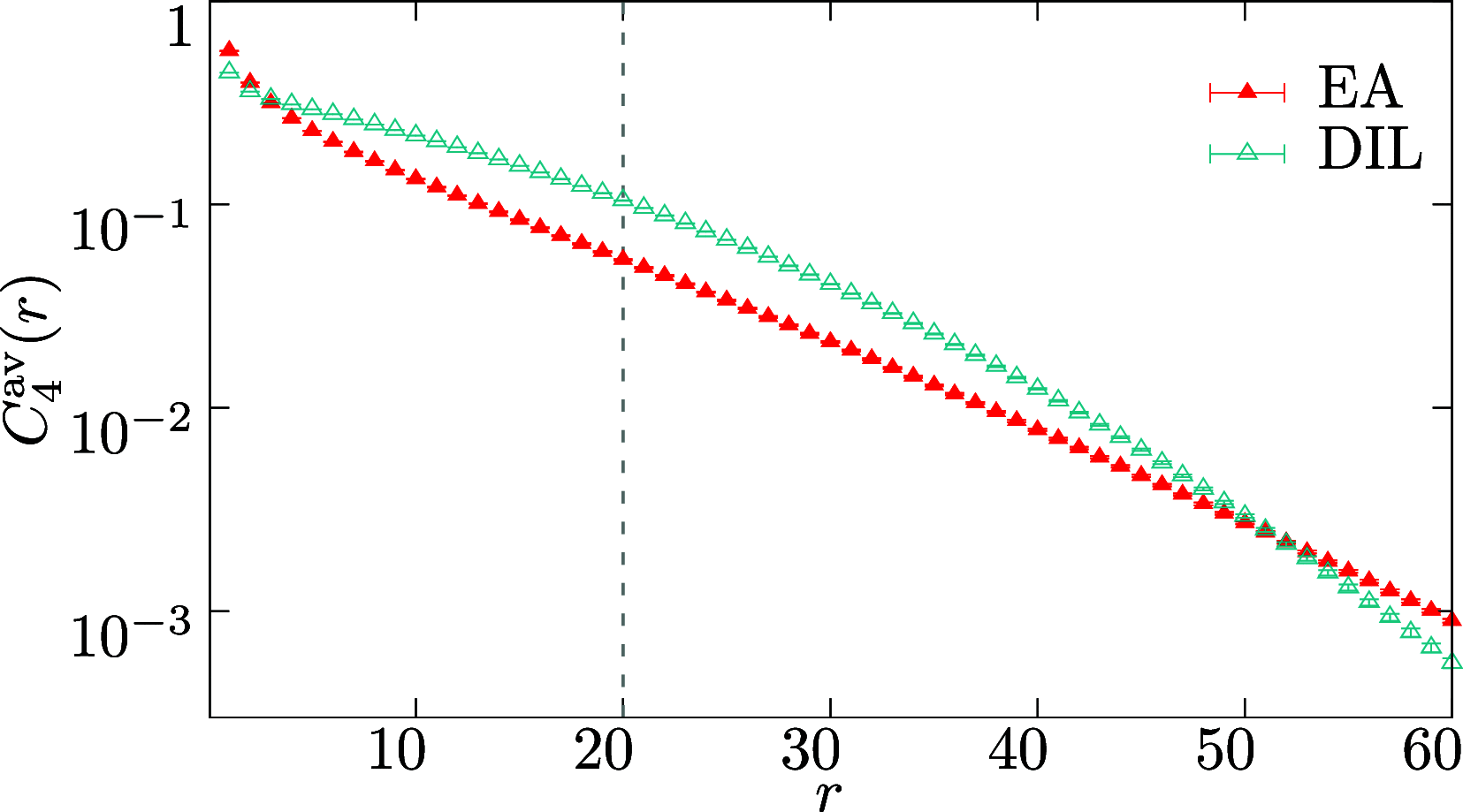
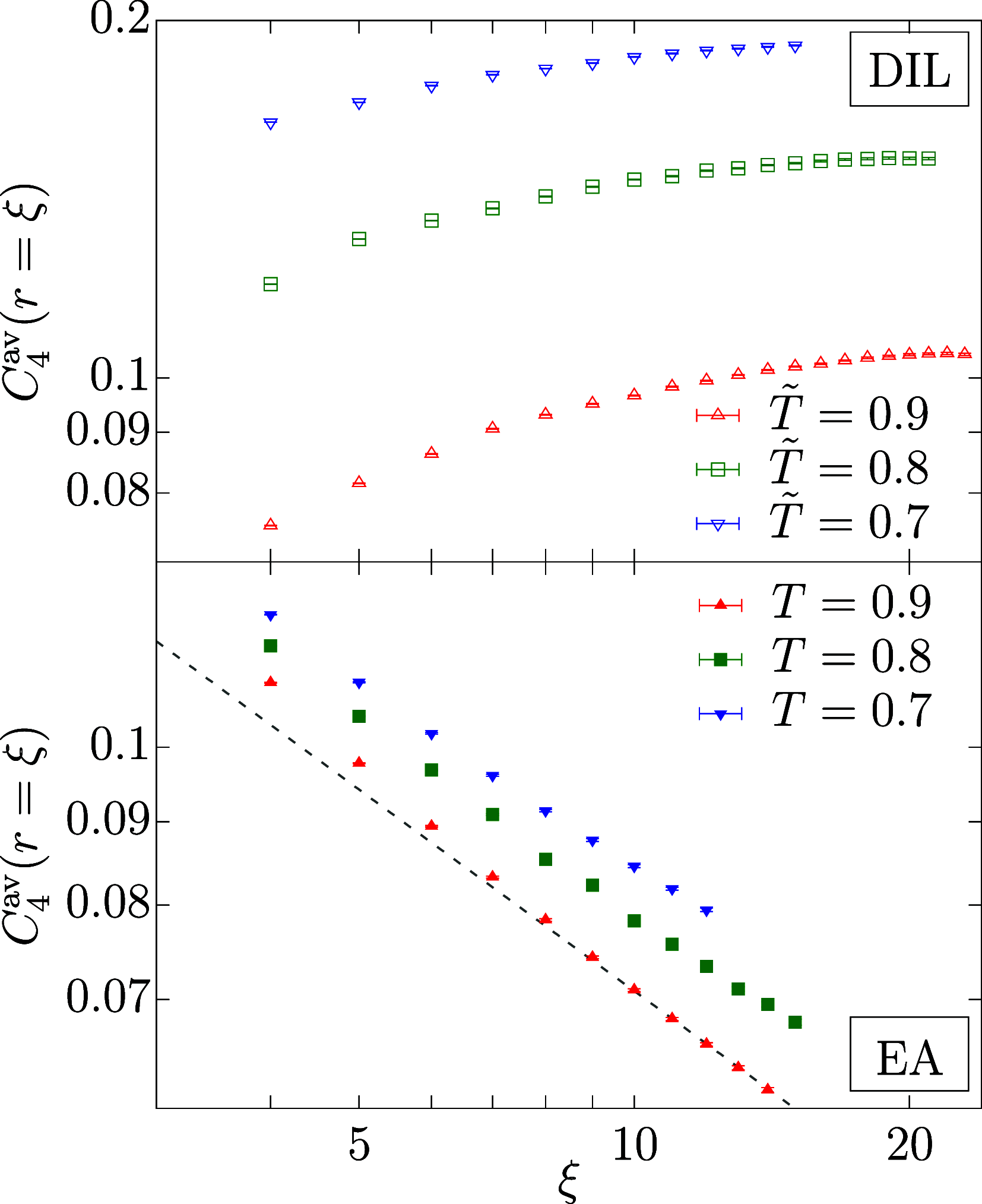
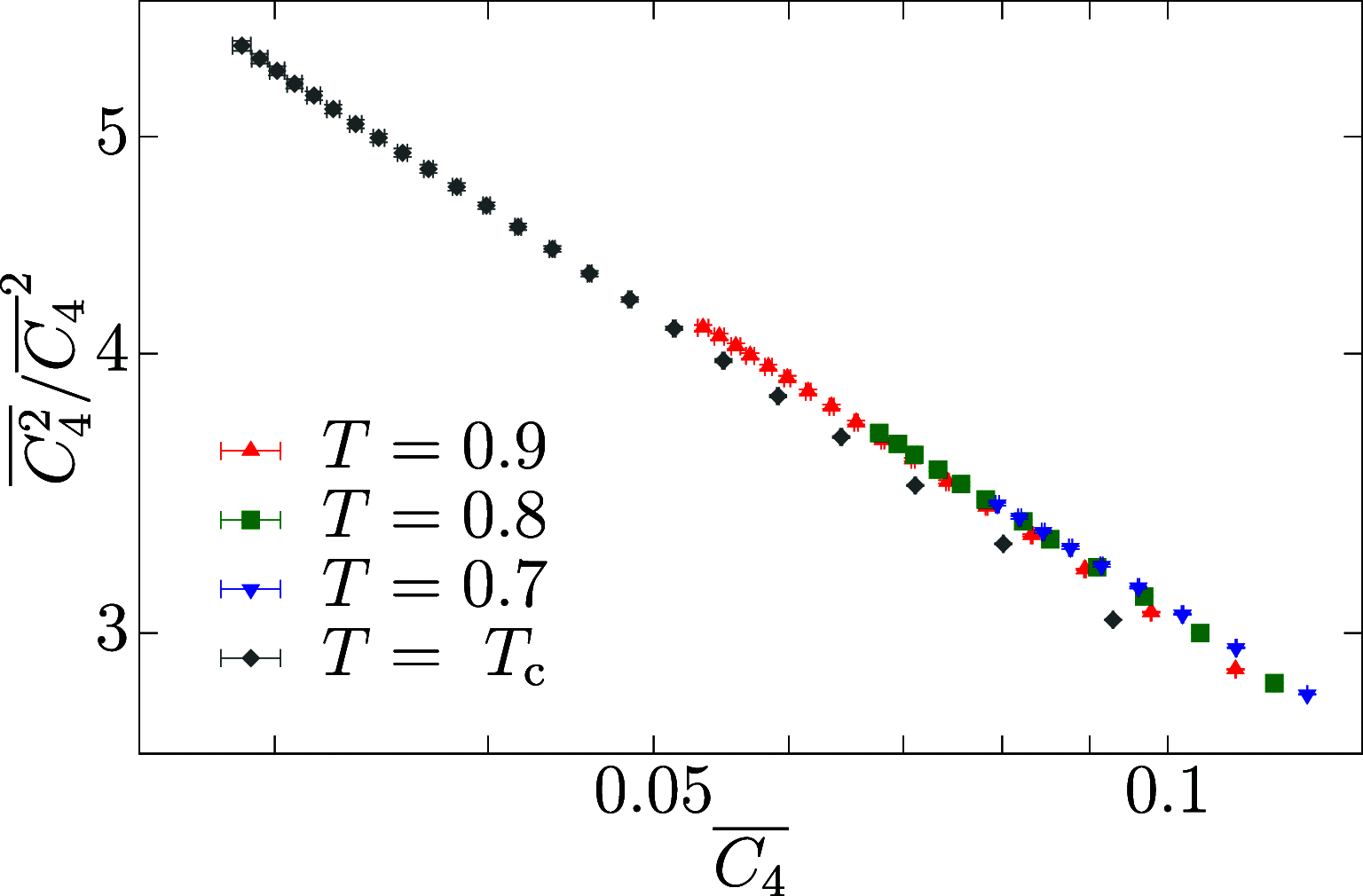
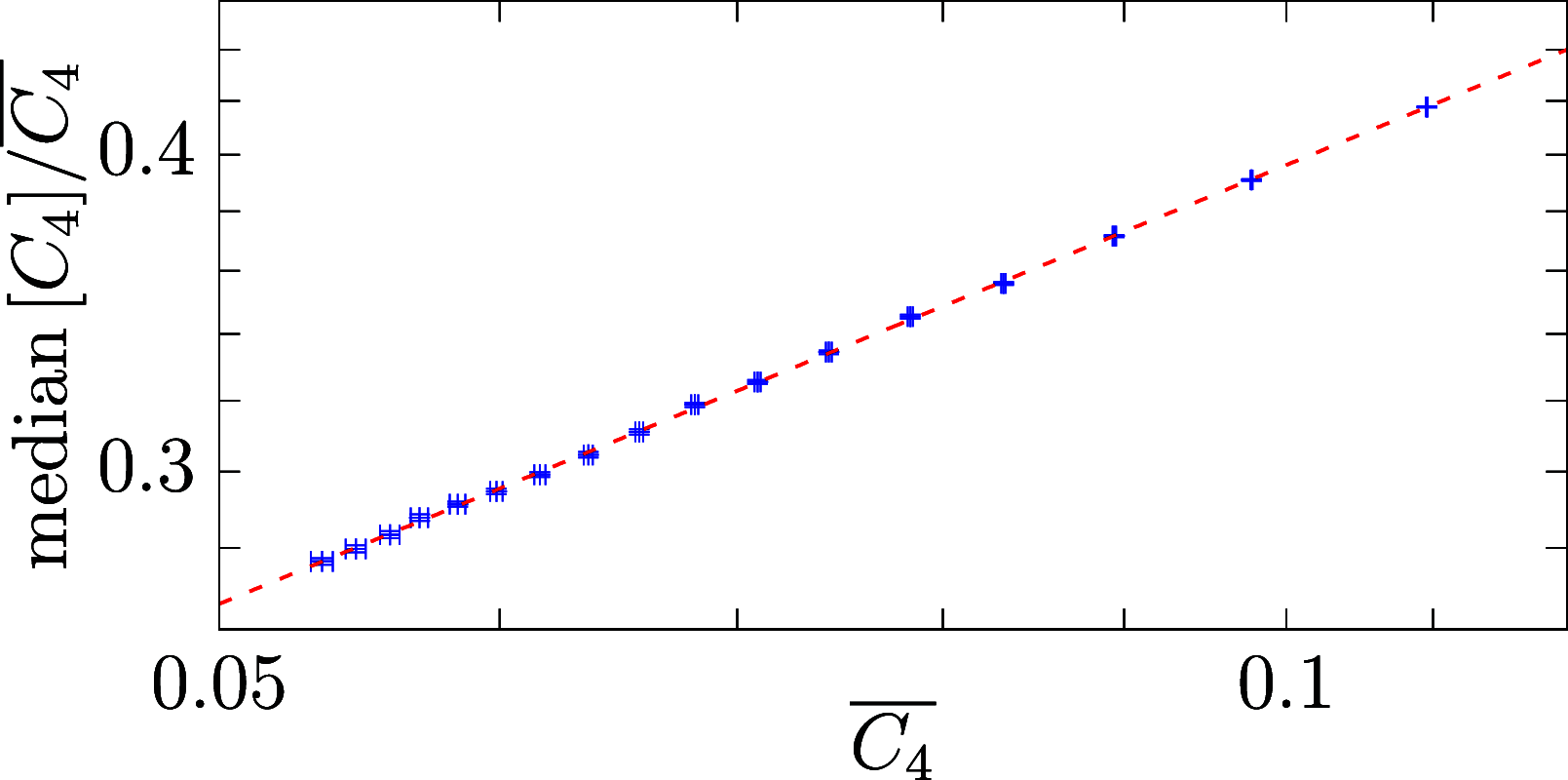
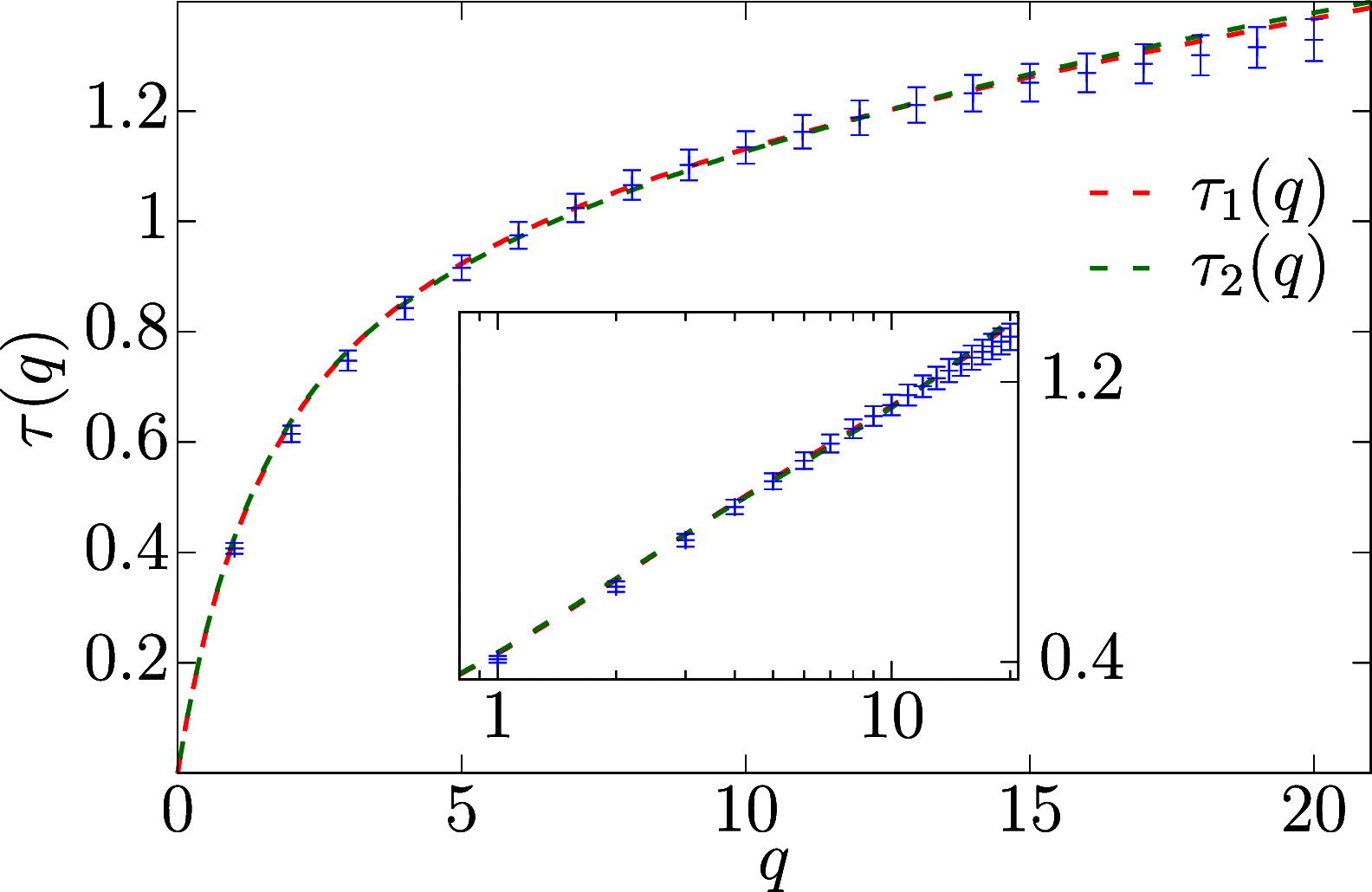
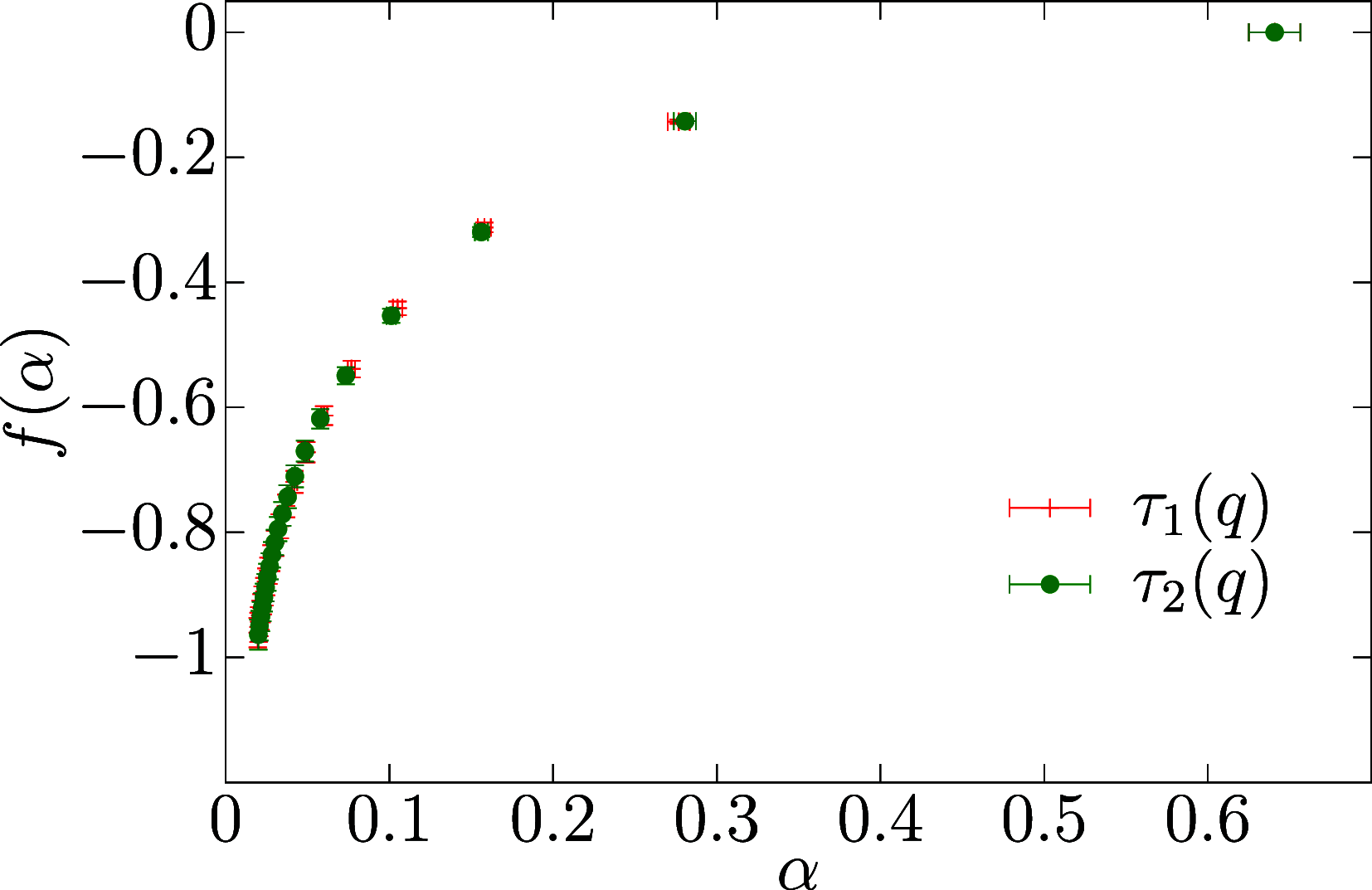
We unveil the multifractal behavior of Ising spin glasses in their low-temperature phase. Using the Janus II custom-built supercomputer, the spin-glass correlation function is studied locally. Dramatic fluctuations are found when pairs of sites at the same distance are compared. The scaling of these fluctuations, as the spin-glass coherence length grows with time, is characterized through the computation of the singularity spectrum and its corresponding Legendre transform. A comparatively small number of site pairs controls the average correlation that governs the response to a magnetic field. We explain how this scenario of dramatic fluctuations (at length scales smaller than the coherence length) can be reconciled with the smooth, self-averaging behavior that has long been considered to describe spin-glass dynamics.

Keywords: disorder systems; fractal dimensions; intermittency; large scale simulations.

Fig. 1.

The correlation function, Eq. 10, as computed for the three-dimensional Ising diluted ferromagnet (DIL) and for the Ising spin glass (EA), versus distance $r$. Data were obtained in systems of linear size $L=160$ with coherence length $\xi (t_{\mathrm{w}})=20$ (dashed vertical line) at temperature $T=0.9$—recall that $T_{\mathrm{c}}\approx 1.1$ for EA (32). As explained in Methods, the coherence length is computed from the integral $I_2={\int }_0^{\infty }{r}^2{C}_4^{\text{av}}(r)\mathrm{d}r$ (the integrand is shown in the SI Appendix).

Fig. 2.

Correlation function $C_4^{\text{av}}(r=\xi (t_{\mathrm{w}}))$, see Eq. 10 versus the coherence length $\xi (t_{\mathrm{w}})$, as computed for DIL (Top) and for EA (Bottom) at temperatures $T,\tilde{T}=0.9,0.8$ and $0.7$ (see Methods for a complete definition of $\tilde{T}$). Error bars are smaller than the point size. The dashed line is our fit to Eq. 2, with $q=1$, for EA at $T=0.9$ (to avoid scaling corrections, we fit in the range $\xi (t_{\mathrm{w}})\in [10,20]$, see SI Appendix for further information). Note that, while the DIL $C_4^{\text{av}}(r=\xi (t_{\mathrm{w}}))$ tends to a $T$-dependent positive limit for large coherence length (which excludes multiscaling at $T<T_{\text{c}}$), the spin-glass correlation functions steadily decrease with $\xi (t_{\mathrm{w}})$.

Fig. 3.

Ratio of the second moment of the spin-glass correlation function $C_4$ computed at $r=\xi (t_{\mathrm{w}})$, $\overline{C_4^2}$, to the squared first moment, ${\overline{C_4}}^2$, as a function of $\overline{C_4}$. We show the data for all temperatures considered in this work. $\overline{C_4}$ tends to zero as the coherence length $\xi (t_{\mathrm{w}})$ gets large, recall Fig. 2. Note that $\overline{C_4^2}/{\overline{C_4}}^2$ scales with $\overline{C_4}$ as a power law, which indicates that in the scaling limit (i.e., $\xi (t_{\mathrm{w}})\to \infty$ or $\overline{C_4}\to 0$) the order of magnitude of $\overline{C_4^2}$ is larger than the one of ${\overline{C_4}}^2$. Data in the glassy phase, $T<T_{\mathrm{c}}$, roughly follow the same scaling curve. At the critical point, there is still a power type relation with a slightly different exponent. Error bars are smaller than the points size. The same data are shown as a function of $\xi (t_{\mathrm{w}})$ in SI Appendix.

Fig. 4.

Grayscale representation of the order-of-magnitude modulating factor $M(\mathit{x},\mathit{r},t_{\mathrm{w}})$, see Eq. 1, computed for site $\mathit{x}=(64,64,64)$ of a sample with coherence length $\xi (t_{\mathrm{w}})=20$, at $T=0.9$, with an $N_{\mathrm{R}}=512$ estimator (Methods). We show results for displacement vectors $\mathit{r}=(r_x,r_y,r_z)$ in a cube $-40\le r_x,r_y,r_z\le 40$. The Top-Left panel depicts the three visible faces of the cube, while the other three panels show sections at $r_z=-20,0,20$, respectively. Our color code is darker the smaller $M(\mathit{x},\mathit{r},t_{\mathrm{w}})$ (hence, the more slowly correlations decay with distance). For ease of representation, we have chosen a color code linear between the minimal value of $M(\mathit{x},\mathit{r},t_{\mathrm{w}})$ and 2.5. Displacements $\mathit{r}$ with $M(\mathit{x},\mathit{r},t_{\mathrm{w}})>2.5$ are depicted as if $M(\mathit{x},\mathit{r},t_{\mathrm{w}})=2.5$. See SI Appendix for more examples of this modulating factor.

Fig. 5.

Median of the distribution $P[C_4(r=\xi )]$ in units of the first moment, $\overline{C_4}(r=\xi )$, versus $\overline{C_4}(r=\xi )$, as computed for the spin glass at temperature $T=0.9$. We show data in the logarithmic scale. Therefore, the dashed line (a power-law fit with exponent $\sim 0.5$, see SI Appendix for details) appears as a straight line.

Fig. 6.

Scaling exponent $\tau (q)$ for the $q$-th moment $\overline{C_4{(r=\xi )}^q}\sim {\xi }^{-\tau (q)}$ computed from simulations of the Ising spin glass at $T=0.9$ (see SI Appendix for results at $T_{\mathrm{c}}$). The nonlinear behavior is a strong indication of multifractality. The dashed lines are fits to the functional forms in Eq. 3 (the goodness-of-fit statistics are presented in the SI Appendix). The inset presents the same data as a function of $log(q)$.

Fig. 7.

Legendre transformation $f(\alpha )$ of function $\tau (q)$, see Eq. 7, as a function $\alpha =\mathrm{d}\tau /\mathrm{d}q$, computed from the fitting ansätze in Eq. 3. Errors on both axes have been obtained as explained in Methods (for further details, see ref. 50). Since $f(\alpha )$ is the large-deviations function of the decay rate $C_4(r=\xi )\sim r^{-\alpha }$, the data show that the majority of sites have the median decay rate of approximately $0.65$, much larger than the mean decay rate $\alpha \approx 0.4$.