A novel technique for delineating the effect of variation in the learning rate on the neural correlates of reward prediction errors in model-based fMRI

Abstract

Introduction: Computational models play an increasingly important role in describing variation in neural activation in human neuroimaging experiments, including evaluating individual differences in the context of psychiatric neuroimaging. In particular, reinforcement learning (RL) techniques have been widely adopted to examine neural responses to reward prediction errors and stimulus or action values, and how these might vary as a function of clinical status. However, there is a lack of consensus around the importance of the precision of free parameter estimation for these methods, particularly with regard to the learning rate. In the present study, I introduce a novel technique which may be used within a general linear model (GLM) to model the effect of mis-estimation of the learning rate on reward prediction error (RPE)-related neural responses.

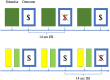
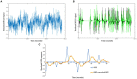
Methods: Simulations employed a simple RL algorithm, which was used to generate hypothetical neural activations that would be expected to be observed in functional magnetic resonance imaging (fMRI) studies of RL. Similar RL models were incorporated within a GLM-based analysis method including derivatives, with individual differences in the resulting GLM-derived beta parameters being evaluated with respect to the free parameters of the RL model or being submitted to other validation analyses.

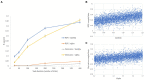
Results: Initial simulations demonstrated that the conventional approach to fitting RL models to RPE responses is more likely to reflect individual differences in a reinforcement efficacy construct (lambda) rather than learning rate (alpha). The proposed method, adding a derivative regressor to the GLM, provides a second regressor which reflects the learning rate. Validation analyses were performed including examining another comparable method which yielded highly similar results, and a demonstration of sensitivity of the method in presence of fMRI-like noise.

Conclusion: Overall, the findings underscore the importance of the lambda parameter for interpreting individual differences in RPE-coupled neural activity, and validate a novel neural metric of the modulation of such activity by individual differences in the learning rate. The method is expected to find application in understanding aberrant reinforcement learning across different psychiatric patient groups including major depression and substance use disorder.

Keywords: fMRI; general linear model; prediction errors; reinforcement learning; reinforcement sensitivity.

Figure 1

Changes in RPE through trials including non-reward (1–9) and reward (10–20) outcomes for a simple conditioning paradigm. Initial Q set to 0.5, lambda set to 1. (A) Variation of RPE with fast (0.7: blue) and slow (0.2: orange) learning rates. Note the slower decline in RPEs in the slow learning rate from trial 10 onwards. (B) Variation in RPE with an intermediate learning rate (0.45: green), and its derivative obtained from the gradient function in MATLAB (purple). (C) The intermediate learning rate RPE displayed in (B), with the derivative added (blue) or subtracted (orange). Note that this broadly captures the predictions of an RPE model with a faster learning rate when added or slower learning rate when subtracted, albeit with some inaccuracies especially on trial 9. (D) Variation in the value of the cue (Q) for the fast (0.7: blue) and slow (0.2: orange) learning rates.

Figure 2

Schematic to show the simulated paradigms employed for the classical conditioning (top) and instrumental paradigms (bottom). In the conditioning paradigm, a cue (here represented as green) predicts an outcome [here represented as a monetary reward ($) or no monetary reward (red X)]. The probability of a rewarding outcome (as opposed to no reward) starts at 0.5, but drifts up or down through the experiment. The instrumental paradigm has a similar design, except that there are two cues which the simulated participant must choose between. These cues have the same cue-outcome probabilities as the conditioning paradigm. Interstimulus interval (ISI), the distance between the outcome events, is 14 s in all cases.

Figure 3

(A) Example of a simulated “ground truth” BOLD signal including RPE responses and fMRI-like noise. (B) Examples of RPE (black) and derivative (green) regressors that would be used to analyze the ground truth timeseries. (C) Figure shows an example of raw RPE signal and HRF-convolved signal for six trials/82 s worth of data for one participant.

Figure 4

(A) Zero-order relationships between lambda/alpha and RPE/derivative-coupled beta parameters, represented in terms of R², across different task durations. Error bars reflect the standard error. (B) Figure displays an example of relationship between lambda and RPE-coupled betas, derived from an analysis including 100 trials worth of data in 5,000 simulated participants. (C) Figure displays an example of relationship between alpha and derivative-coupled betas from the same analysis as (B).