Ultrasound Shear Elastography With Expanded Bandwidth (USEWEB): A Novel Method for 2D Shear Phase Velocity Imaging of Soft Tissues
- PMID: 38198276
- PMCID: PMC11107799
- DOI: 10.1109/TMI.2024.3352097
Ultrasound Shear Elastography With Expanded Bandwidth (USEWEB): A Novel Method for 2D Shear Phase Velocity Imaging of Soft Tissues
Abstract
Ultrasound shear wave elastography (SWE) is a noninvasive approach for evaluating mechanical properties of soft tissues. In SWE either group velocity measured in the time-domain or phase velocity measured in the frequency-domain can be reported. Frequency-domain methods have the advantage over time-domain methods in providing a response for a specific frequency, while time-domain methods average the wave velocity over the entire frequency band. Current frequency-domain approaches struggle to reconstruct SWE images over full frequency bandwidth. This is especially important in the case of viscoelastic tissues, where tissue viscoelasticity is often studied by analyzing the shear wave phase velocity dispersion. For characterizing cancerous lesions, it has been shown that considerable biases can occur with group velocity-based measurements. However, using phase velocities at higher frequencies can provide more accurate evaluations. In this paper, we propose a new method called Ultrasound Shear Elastography with Expanded Bandwidth (USEWEB) used for two-dimensional (2D) shear wave phase velocity imaging. We tested the USEWEB method on data from homogeneous tissue-mimicking liver fibrosis phantoms, custom-made viscoelastic phantom measurements, phantoms with cylindrical inclusions experiments, and in vivo renal transplants scanned with a clinical scanner. We compared results from the USEWEB method with a Local Phase Velocity Imaging (LPVI) approach over a wide frequency range, i.e., up to 200-2000 Hz. Tests carried out revealed that the USEWEB approach provides 2D phase velocity images with a coefficient of variation below 5% over a wider frequency band for smaller processing window size in comparison to LPVI, especially in viscoelastic materials. In addition, USEWEB can produce correct phase velocity images for much higher frequencies, up to 1800 Hz, compared to LPVI, which can be used to characterize viscoelastic materials and elastic inclusions.
Figures




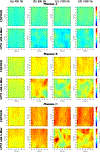









References
-
- Bercoff J, Tanter M, and Fink M, “Supersonic shear imaging: A new technique for soft tissue elasticity mapping,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 51, no. 4, pp. 396–409, Apr. 2004. - PubMed
-
- Bota S et al., “Meta-analysis: ARFI elastography versus transient elastography for the evaluation of liver fibrosis,” Liver Int, vol. 33, no. 8, pp. 1138–1147, Sep. 2013. - PubMed
-
- Sebag F et al., “Shear wave elastography: A new ultrasound imaging mode for the differential diagnosis of benign and malignant thyroid nodules,” J. Clin. Endocrinol. Metabolism, vol. 95, no. 12, pp. 5281–5288, 2010. - PubMed

