Synthesis of causal and surrogate models by non-equilibrium thermodynamics in biological systems

Abstract

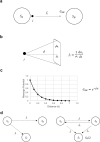
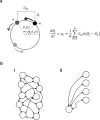
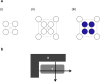
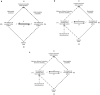
We developed a model to represent the time evolution phenomena of life through physics constraints. To do this, we took into account that living organisms are open systems that exchange messages through intracellular communication, intercellular communication and sensory systems, and introduced the concept of a message force field. As a result, we showed that the maximum entropy generation principle is valid in time evolution. Then, in order to explain life phenomena based on this principle, we modelled the living system as a nonlinear oscillator coupled by a message and derived the governing equations. The governing equations consist of two laws: one states that the systems are synchronized when the variation of the natural frequencies between them is small or the coupling strength through the message is sufficiently large, and the other states that the synchronization is broken by the proliferation of biological systems. Next, to simulate the phenomena using data obtained from observations of the temporal evolution of life, we developed an inference model that combines physics constraints and a discrete surrogate model using category theory, and simulated the phenomenon of early embryogenesis using this inference model. The results show that symmetry creation and breaking based on message force fields can be widely used to model life phenomena.

Figure 1

Message force field (a) The message i generated by system S_A spreads by diffusion, producing a diffuse flow J_i. The system S_B receiving the message changes its state under the force of G_AB (b). The diffusion flow J_i is expressed as $\frac{1}{\mathcal{A}}\frac{\text{d}{n}_i}{\text{d}t}$, depending on the message quantity n_i passing through a unit area (⍲) in a certain direction in a unit time. (c) The force G_AB that changes the state of the system S_B receiving the message is exponentially dependent on the distance between the system S_A and the system S_B. (d) Consider the case where system S_B and system S_C receive a message i generated by system S_A and a message k generated by system S_B. In this case, the force G_k that changes the state of system S_C by message k is subject to the interference of J_i.

Figure 2

Synchronization of limit-cycle oscillators by message (a) If the natural frequency of oscillator x is ${\omega }_x$ and oscillators j and k are coupled by a G_jk force, the phase (θ) of oscillator j with N oscillators interacting by messages is shown as $\frac{d{\theta }_j}{\mathit{dt}}={\omega }_i+\frac{1}{N}\sum _{k=1}^N{G}_{\mathit{jk}}h\left({\theta }_j-{\theta }_k\right)$. (b) Biological systems form a variety of network structures. Here, we show a network structure in which elements are globally coupled and in which the network structure changes dynamically, as in the case of somite formation.

Figure 3

Spontaneous symmetry breaking due to cell proliferation and differentiation. (a) When cells in the same state come together to form a cluster, there is a difference in the message force field between the inside and outside of the cluster. In (i), all cells receive three streams of messages. In contrast, in (ii), the outer cells receive a flow of three messages, while the inner cells receive a flow of four messages. As a result, the cells inside and outside change to different states, and two populations of cells emerge. (b) When two different cell types proliferate to form two clumps X and Y, respectively, and are subsequently able to exchange messages with each other, a message force field is formed on different spatial axes, depending on the arrangement of the two clumps.

Figure 4

Isomorphism of different biological models The dynamic discrete model allows us to synthesize three different biological models. Consider the case of a biological system transitioning from state A to state B. In the surrogate model, the transition from state A to state B is represented by the state transition probability (a). In the causal model, on the other hand, the outcome of state B is considered to result from a certain cause for the precondition of state A (b). The message force field model explains that an irreversible change from state A to state B occurs within the constraints of the maximum entropy generation principle (c). The symmetry generated by the maximum entropy generation principle is broken by the change in the message force field.

Figure 5

Synthesis of the model based on category theory Time evolution phenomena in biological systems are generally represented as attractor state transitions (i). To make this model versatile, it is necessary to standardize the identification of attractor states (ii). System identification is based on natural language-based types in the case of causal models (iii), feature vectors in the case of machine-learning-generated surrogate models (iv), and message networks in the case of message force field models (v). State transitions are represented by mechanistic constraints in the causal model (vi), by probabilities in the surrogate model (vii), and by the maximum entropy generation principle and synchrony breaking in the message force field (viii). To map the three models, we formulate them using the adjunction of category theory. The functor F from category (C) of the causal model to category (D) of the surrogate model and the functor G from category (D) of the surrogate model to category (C) of the causal model are adjoined. Similarly, bidirectional functor (I, H) from the category (C) of causal models and the category (E) of message force field models and bidirectional functor (O, P) from the category (D) of surrogate models and the category (E) of message force field models are adjoined.

Figure 6

Inference of the blastocyst differentiation induction process by integrating the surrogate model and the message force field model. (a) The state changes of the embryo from fertilized egg to blastocyst are modeled based on the surrogate model as six different discrete states: fertilized egg (i), 2-cell stage (ii), 4-cell stage (iii), 8-cell stage (iv), compaction (v), and 16-cell stage (vi). (b) Cells from 2-cell stage to 8-cell stage express seven growth factors and six growth receptors. The synchronized cell division that occurs during this process is caused by the binding force expressed by the binding constants of the growth factors. (c) Compaction increases cell–cell adhesion and alters the force field of the message. The force field generated is asymmetric between inside and outside, resulting in the localization of cdx2 transcripts to the outside of the cell mass. As a result, an inner cell mass is induced in the interior and a trophic ectoderm is induced in the exterior. This process can be described as the breaking of synchrony and the reestablishment of synchrony.