A hybrid approach to dynamic cognitive psychometrics : Dynamic cognitive psychometrics

Abstract

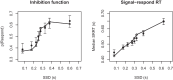
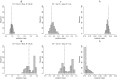
Dynamic cognitive psychometrics measures mental capacities based on the way behavior unfolds over time. It does so using models of psychological processes whose validity is grounded in research from experimental psychology and the neurosciences. However, these models can sometimes have undesirable measurement properties. We propose a "hybrid" modeling approach that achieves good measurement by blending process-based and descriptive components. We demonstrate the utility of this approach in the stop-signal paradigm, in which participants make a series of speeded choices, but occasionally are required to withhold their response when a "stop signal" occurs. The stop-signal paradigm is widely used to measure response inhibition based on a modeling framework that assumes a race between processes triggered by the choice and the stop stimuli. However, the key index of inhibition, the latency of the stop process (i.e., stop-signal reaction time), is not directly observable, and is poorly estimated when the choice and the stop runners are both modeled by psychologically realistic evidence-accumulation processes. We show that using a descriptive account of the stop process, while retaining a realistic account of the choice process, simultaneously enables good measurement of both stop-signal reaction time and the psychological factors that determine choice behavior. We show that this approach, when combined with hierarchical Bayesian estimation, is effective even in a complex choice task that requires participants to perform only a relatively modest number of test trials.

Keywords: Choice behavior; Cognitive psychometrics; Reaction times; Response inhibition; Stop-signal paradigm.

Fig. 1

Schematic representation of the trial types in the stop-signal paradigm. SSD: stop-signal delay. Figure available at https://flic.kr/p/2n1oRSe under a CC-BY 2.0 license (https://creativecommons.org/licenses/by/2.0/)

Fig. 2

The left panel shows the evidence-accumulation process on go trials, with the choice stimulus presented at $t=0$. Once the stimulus is encoded, two evidence accumulators (runners) corresponding to each response option start to race each other from the same initial level. The runner that crosses its response threshold first wins the race and triggers the associated response. The jiggly lines show ten races between the runner that matches (blue) and the one that mismatches (red) the choice stimulus. Here the thresholds are assumed to be the same and correspond to the time axis, but the thresholds of the two accumulators may differ. The dashed lines show the finishing time distribution of each runner across trials, which are longer for the red “mismatch” accumulator as it has a lower average accumulation rate. The solid lines show the distribution of observed “winning” times where the corresponding runner finished first; these are shorter than the finishing times because faster runners win races. The right panel shows these distributions on stop trials, where the presentation of the choice stimulus is followed at $t=SSD$ by a stop signal that triggers the stop runner. The dashed lines show the finishing time distributions, with the gray line depicting the ex-Gaussian stop runner. The solid lines represent the winning times of the go runners, i.e., the distribution of finishing times where the corresponding go runner was fast enough to beat the other go runner and the stop runner. These winning times are faster for stop than for go trials because slower go finishing times tend to lose the race to the stop runner. The winning times for the stop runner (i.e., finishing times that were fast enough to beat both go runners) are not shown because the stop runner does not produce overt responses, so this distribution is unobserved. SSD: stop-signal delay. Figure available at https://flic.kr/p/2mXYBbh under a CC-BY 2.0 license (https://creativecommons.org/licenses/by/2.0/)

Fig. 3

Example of the choice stimulus on go trials (left) and the choice stimulus followed by the stop signal on stop trials (right). Each cell in the 20 $\times$ 20 checkerboard is randomly colored blue or orange. The difficulty factor determines the proportion of cells colored by the dominant color: 54% in the easy condition and 52% in the hard condition

Fig. 4

Cumulative distribution functions for the observed go RTs and signal-respond RTs (thick lines; open circles show the ${10}^{\mathit{th}}$, ${30}^{\mathit{th}}$, ${50}^{\mathit{th}}$, ${70}^{\mathit{th}}$, and ${90}^{\mathit{th}}$ percentiles) and for the model fits (thin lines; grey points show predictions resulting from the 100 posterior predictive samples, with solid points showing their average). Each panel contains results for BLUE and ORANGE responses. Panel titles indicate stimulus (blue vs. orange), bias (blue vs. orange), and trial type (GO vs. SS = stop signal). The results are collapsed over the difficulty and block type manipulations

Fig. 5

Observed vs. predicted inhibition function (left panel) and median signal-respond RTs (right panel). Observed data are shown with open circles joined by lines. Model fits are shown with solid points, with the 95% credible intervals obtained based on predictions resulting from the 100 posterior predictive samples. SSD = stop-signal delay; p(Respond) = probability of responding on stop trials; SRRT = signal-respond RT

Fig. 6

Parameter-recovery results. Results for the go and trigger failure parameters $P_{\mathit{GF}}$ and $P_{\mathit{TF}}$ are presented on the probability scale. See text for details

Fig. 7

Distribution of the posterior mean across 200 replicated data sets for the threshold B, evidence-accumulation rate v, and non-decision time $t_0$ parameters. The vertical dashed lines show the true values. Block type (BT) = trialwise, bias (B) = blue, accumulator (R) = BLUE, difficulty (D) = easy, and accumulator match (M) = true, corresponding to the accumulator matching the stimulus. The top row shows a parameter setting resulting in excellent parameter recovery, where the distribution of posterior means is unimodal and centered around the true data-generating value for all parameters. The bottom row shows a parameter setting with poor recovery, with bimodality in the distribution of the posterior means of the go parameters. For both parameter settings, the figure shows three out of the 22 parameters, one for each parameter type (i.e., evidence-accumulation rate, threshold, and non-decision time). The full parameter set for all 18 parameter settings are presented in the Supplementary Materials

Fig. 8

Posterior distributions for nine replications (shown with different colors) of fitting the RDEX model to empirical data. The top row shows the posterior distributions resulting from individual estimation, and the bottom row shows the posterior distributions of the same participant resulting from hierarchical estimation. For brevity, only three of the 22 parameters are presented: B, v, and $t_0$. Block type = blockwise, bias = blue, accumulator = orange, difficulty = easy, and accumulator match = true, corresponding to the accumulator matching the stimulus