Encoding a magic state with beyond break-even fidelity
- PMID: 38200302
- PMCID: PMC10781628
- DOI: 10.1038/s41586-023-06846-3
Encoding a magic state with beyond break-even fidelity
Abstract
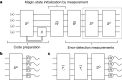
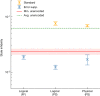
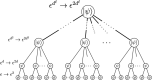
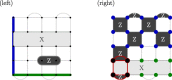
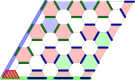
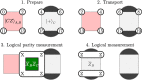
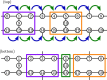
To run large-scale algorithms on a quantum computer, error-correcting codes must be able to perform a fundamental set of operations, called logic gates, while isolating the encoded information from noise1-8. We can complete a universal set of logic gates by producing special resources called magic states9-11. It is therefore important to produce high-fidelity magic states to conduct algorithms while introducing a minimal amount of noise to the computation. Here we propose and implement a scheme to prepare a magic state on a superconducting qubit array using error correction. We find that our scheme produces better magic states than those that can be prepared using the individual qubits of the device. This demonstrates a fundamental principle of fault-tolerant quantum computing12, namely, that we can use error correction to improve the quality of logic gates with noisy qubits. Moreover, we show that the yield of magic states can be increased using adaptive circuits, in which the circuit elements are changed depending on the outcome of mid-circuit measurements. This demonstrates an essential capability needed for many error-correction subroutines. We believe that our prototype will be invaluable in the future as it can reduce the number of physical qubits needed to produce high-fidelity magic states in large-scale quantum-computing architectures.
© 2024. The Author(s).
Conflict of interest statement
A patent (application no. 18/053087) was filed on 7 November 2022 with listed inventors B.J.B., A.W.C., R.S.G., T.J.-O. and T.J.Y. The authors declare no other competing financial or non-financial interests.
Figures


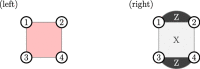


References
-
- Ryan-Anderson C, et al. Realization of real-time fault-tolerant quantum error correction. Phys. Rev. X. 2021;11:041058.
LinkOut - more resources
Full Text Sources

