Multispherical shapes of vesicles with intramembrane domains

Abstract

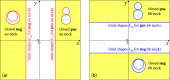
Phase separation of biomembranes into two fluid phases, a and b, leads to the formation of vesicles with intramembrane a- and b-domains. These vesicles can attain multispherical shapes consisting of several spheres connected by closed membrane necks. Here, we study the morphological complexity of these multispheres using the theory of curvature elasticity. Vesicles with two domains form two-sphere shapes, consisting of one a- and one b-sphere, connected by a closed ab-neck. The necks' effective mean curvature is used to distinguish positive from negative necks. Two-sphere shapes of two-domain vesicles can attain four different morphologies that are governed by two different stability conditions. The closed ab-necks are compressed by constriction forces which induce neck fission and vesicle division for large line tensions and/or large spontaneous curvatures. Multispherical shapes with one ab-neck and additional aa- and bb-necks involve several stability conditions, which act to reduce the stability regimes of the multispheres. Furthermore, vesicles with more than two domains form multispheres with more than one ab-neck. The multispherical shapes described here represent generalized constant-mean-curvature surfaces with up to four constant mean curvatures. These shapes are accessible to experimental studies using available methods for giant vesicles prepared from ternary lipid mixtures.

Fig. 1

Domain-induced budding of giant unilamellar vesicles (GUVs) as predicted by theory [22, 23] and observed by fluorescence microscopy [4, 7, 10]. The two intramembrane domains consist of liquid-disordered (Ld) and liquid-ordered (Lo) lipid phases: a Cross-section through a vesicle that formed two lipid phase domains after a decrease in temperature. Reprinted with permission from Ref.  [4] (Copyright 2003, Springer-Nature); b Three-dimensional confocal scan of a two-domain vesicle that was formed by electrofusion. Reprinted with permission from Ref.  [7] (Copyright 2006, WSPC); and c Cross-section through a two-domain vesicle after osmotic deflation. Reprinted with permission from Ref.  [10] (Copyright 2021, Wiley) In each example, two different membrane dyes have been used to distinguish the Ld and Lo domains by fluorescence microscopy. The Ld phase is red in (a, b) and orange in (c), the Lo phase is blue in (a) and green in (b, c). Because the line tension of a domain boundary is positive, this boundary can reduce its line energy by constricting the vesicle via an open membrane neck. Scale bars: 5 $\mu$m in (a) and $10\mu$m in (c)

Fig. 2

Multispherical shapes of GUVs with laterally uniform membranes: a Two-sphere shape consisting of one large and one small sphere, forming an out-bud; b Two-sphere shape with one large and one small sphere, forming an in-bud; c multisphere with one large sphere and a linear chain of six outward-pointing small spheres; d Multisphere with one large sphere and a linear chain of six inward-pointing small spheres; e Multisphere consisting of two large and one small spheres; f Multisphere with two large and two small spheres; and g Multisphere consisting of 24 equally sized spheres. In (a), (c), (e)–(g), all spheres have a positive mean curvature which implies that the membranes have a positive spontaneous curvature. In (b) and (d), the mean curvature of the small spheres is negative caused by a negative spontaneous curvature. All scale bars are 10 $\mu$m [25]

Fig. 3

Different types of two-sphere shapes formed by vesicles with one a-domain (red) and one b-domain (blue). The radius of the a-sphere is denoted by $R_a$, the radius of the b-sphere by $R_b$: a, b Out-budded two-sphere shapes with $R_a>R_b$ in (a) and $R_b>R_a$ in (b); and (c, d) In-budded two-sphere shapes with $R_a>R_b$ in (c) and $R_b>R_a$ in (d) All four two-sphere vesicles have the same membrane area A but the vesicle volumes in (a, b) are larger than those in (c, d). The dashed vertical lines represent axes of rotational symmetry. The interior and exterior compartments are distinguished by cyan and white color, respectively

Fig. 4

Formation of two-sphere shapes with positive ab-necks by osmotic deflation ($\to$), which reduces the vesicle volume whereas osmotic inflation ($\leftarrow$) increases this volume: a, b When deflated, a spherical two-domain vesicle with rescaled volume $v=1$ and area fraction ${\mathrm{\Phi }}_b=9/25=0.36$ forms a two-sphere shape with one out-budded a-sphere of radius $r_a=4/5$ and one out-budded b-sphere of radius $r_b=3/5$, thereby reducing the rescaled volume from $v=1$ to $v=91/125=0.728$; and c, d Deflation of a spherical two-domain vesicle with rescaled volume $v=1$ and area fraction ${\mathrm{\Phi }}_b=1/17=0.05882$ creates a two-sphere shape with one out-budded a-sphere of radius $r_a=4/{17}^{1/2}$, one out-budded b-sphere of radius $r_b=1/{17}^{1/2}$, and rescaled volume $v=65/{17}^{3/2}=0.9273$. Inflation of the two-sphere shapes in (b) and (d) leads back to the spherical two-domain vesicles in (a) and (c)

Fig. 5

Formation of two-sphere shapes with an in-budded b-domain (blue) by osmotic deflation ($\to$), which reduces the vesicle volume whereas osmotic inflation ($\leftarrow$) increases this volume: a, b When deflated, a spherical two-domain vesicle with rescaled volume $v=1$ and area fraction ${\mathrm{\Phi }}_b=9/25=0.36$ forms a two-sphere shape with one a-sphere of radius $r_a=4/5$ and one in-budded b-sphere of radius $r_b=3/5$, thereby reducing the rescaled volume to $v=37/125=0.296$; and c, d Deflation of a spherical two-domain vesicle with rescaled volume $v=1$ and area fraction ${\mathrm{\Phi }}_b=1/17=0.05882$ creates a two-sphere shape with one a-sphere of radius $r_a=4/{17}^{1/2}$, one in-budded b-sphere of radius $r_b=1/{17}^{1/2}$ and the rescaled volume $v=63/{17}^{3/2}=0.8988$. Inflation of the two-sphere shapes in (b) and (d) leads back to the single spheres in (a) and (c)

Fig. 6

Stability regimes (yellow) for closed ab-necks of two-sphere vesicles within the morphology diagrams defined by the coordinates $x\equiv {\overline{m}}_a$ and $y\equiv {\overline{m}}_b$. All two-domain vesicles have the same area fraction ${\mathrm{\Phi }}_b=0.36$: a Stability regime for positive ab-necks of two-sphere vesicles with positive mean curvature $M_a>0$ of the a-sphere, positive mean curvature $M_b>0$ of the b-sphere, and positive effective mean curvature $M_{\mathit{ab}}^{\text{eff}}>0$ of the ab-neck as in Eq. (27); and b Stability regime for negative ab-necks of two-sphere vesicles with in-budded b-domains (blue), corresponding to positive mean curvature $M_a>0$ of the a-sphere, negative mean curvature $M_b<0$ of the b-sphere, and negative effective mean curvature $M_{\mathit{ab}}^{\text{eff}}<0$ of the ab-neck as in Eq. (28). In (a), all vesicles have constant volume $v=0.728$ as in Fig. 4b. In (b), all vesicles have constant volume $v=0.296$ as in Fig. 5b. In both panels, the line of limit shapes $L_{\mathit{ab}}$ (purple) separates vesicle shapes with stably closed necks from those with open necks. The intercepts of these $L_{\mathit{ab}}$-lines with the coordinate axes are denoted by $y_{\mathit{ab}}={\overline{m}}_{b,ab}$ and $x_{\mathit{ab}}={\overline{m}}_{a,ab}$. For out-budded shapes as in (a), these intercepts are given by Eqs. (50) and (51); for in-budded shapes as in (b), they are provided by Eqs. (59) and (60) further below

Fig. 7

Some examples for multspherical shapes formed by two-domain vesicles. Each multisphere has a single ab-neck that contains the domain boundary between the a- and b-domain: a, b Four-sphere shapes with two a- and two b-spheres connected by one aa-neck and one bb-neck; and c, d Seven-sphere shapes with three a- and four b-spheres connected by two aa-necks and three bb-necks. In the examples displayed here, the a- and b-sphere connected by the ab-neck have positive mean curvatures which implies that each ab-neck is positive. Multispheres with negative ab-necks are discussed further below, see Sect. 6.2 and Fig. 11

Fig. 8

Some examples for multispherical shapes with two ab-necks that can be formed by vesicles with three domains in chemical equilibrium: a Three-sphere vesicles with one a-sphere (red) and two b-spheres (blue); b–d Multisphere vesicles with one cluster of three a-spheres (red) and two clusters of b-spheres (blue). Chemical equilibrium implies that, in each panel, the two b-clusters consist of large and small spheres with identical mean curvatures. Both ab-necks are positive in all four panels. In (c) and (d), the bb-necks are negative. In (d), the aa-necks are negative as well

Fig. 9

Morphology diagrams with coordinates $x={\overline{m}}_a$ and $y={\overline{m}}_b$: a Stability regimes (yellow) for positive and negative aa-necks. For positive aa-necks, the spontaneous curvature ${\overline{m}}_a\ge {\overline{M}}_{\mathit{aa}}^{\text{eff}}>0$ as in Eq. (86), which defines the right stability regime. For negative aa-necks, the spontaneous curvature ${\overline{m}}_a\le {\overline{M}}_{\mathit{aa}}^{\text{eff}}<0$ as in Eq. (87), leading to the left stability regime. Because the left and the right stability regime have no overlap, all aa-necks must be either positive or negative; and b Stability regimes (yellow) for positive and negative bb-necks. For positive bb-necks, the spontaneous curvature ${\overline{m}}_b\ge {\overline{M}}_{\mathit{bb}}^{\text{eff}}>0$ as in Eq. (88), corresponding to the upper stability regime. For negative bb-necks, the spontaneous curvature ${\overline{m}}_a\le {\overline{M}}_{\mathit{aa}}^{\text{eff}}<0$ as in Eq. (89), which defines the lower stability regime. Because the lower and the upper stability regime have no overlap, all bb-necks must be either positive or negative

Fig. 10

Four-sphere shapes and their stability regimes for positive ab-necks. The multispheres consist of one a-domain (red) and one b-domain (blue) forming two a-spheres and two b-spheres: a Positive aa-neck and positive bb-neck; b positive aa-neck and negative bb-neck; c negative aa-neck and positive bb-neck; and d Negative aa-neck and negative bb-neck. The bottom row displays the stability regimes (yellow) within the morphology diagrams defined by the rescaled spontaneous curvatures $x={\overline{m}}_a$ and $y={\overline{m}}_b$. The purple, red, and blue lines represent the lines of limit shapes $L_{\mathit{ab}}$, $L_{\mathit{aa}}$, and $L_{\mathit{bb}}$, respectively, which provide the boundaries for the stability regimes. In (d), the three lines lead to a small, triangular stability regime, which requires fine-tuning of both spontaneous curvatures

Fig. 11

Four-sphere shapes and their stability regimes for negative ab-necks. The multispheres consist of one a-domain (red) and one in-budded b-domain (blue), forming two a-spheres and two b-spheres: a Negative aa-neck and negative bb-neck; b Positive aa-neck and negative bb-neck; c Negative aa-neck and positive bb-neck; and d Positive aa-neck and positive bb-neck. The subpanels in the bottom row display the corresponding stability regimes (yellow) within the morphology diagram defined by the rescaled spontaneous curvatures $x={\overline{m}}_a$ and $y={\overline{m}}_b$. The purple, red, and blue lines represent the lines of limit shapes $L_{\mathit{ab}}$, $L_{\mathit{aa}}$, and $L_{\mathit{bb}}$, respectively, which provide the boundaries for the stability regimes of the four-sphere shapes. In (d), the three lines lead to a small, triangular stability regime, which requires fine-tuning of both spontaneous curvatures

Fig. 12

Trasformation of nested multi-domain vesicles into nested multispheres: a a spherical three-domain vesicle consisting of a large $a_1$-domain (red) on the southern hemisphere, a smaller ring-like $b_1$-domain (blue) on the northern hemisphere, and an even smaller $a_2$-domain (red) close to the north pole. Deflation of such a three-domain vesicle can lead to the nested multisphere in (b) with an outer $a_1$-sphere, an in-budded $b_1$-sphere, and an out-budded $a_2$-sphere; and c a spherical four-domain vesicle consisting of a large $a_1$-domain (red), a ring-like $b_1$-domain (blue), a ring-like $a_2$-domain (red), and a $b_2$-domain (blue) close to the north pole. For simplicity, the three- and four-domain vesicles in (a) and (c) are taken to be axisymmetric, which implies that the nested domains are concentric as well. However, shifting the concentric domains against each other will again lead to nested multispheres, which are quite similar to those in (b) and (d)

Fig. 13

Multispherical limit of triunduloids: a, b Triunduloids with open membrane necks as studied in differential geometry. Reprinted with permission from Ref.  [40] (Copyright 1997, Springer-Verlag); and c Triunduloid built up from punctured spheres which are connected by closed necks. The central sphere is connected to three adjacent spheres by three necks