How is Membrane Permeation of Small Ionizable Molecules Affected by Protonation Kinetics?
- PMID: 38227958
- PMCID: PMC11702507
- DOI: 10.1021/acs.jpcb.3c06765
How is Membrane Permeation of Small Ionizable Molecules Affected by Protonation Kinetics?
Abstract
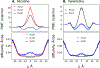
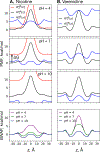
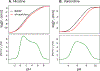
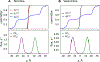
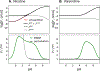
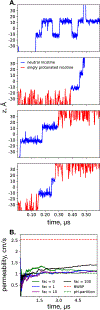
According to the pH-partition hypothesis, the aqueous solution adjacent to a membrane is a mixture of the ionization states of the permeating molecule at fixed Henderson-Hasselbalch concentrations, such that each state passes through the membrane in parallel with its own specific permeability. An alternative view, based on the assumption that the rate of switching ionization states is instantaneous, represents the permeation of ionizable molecules via an effective Boltzmann-weighted average potential (BWAP). Such an assumption is used in constant-pH molecular dynamics simulations. The inhomogeneous solubility-diffusion framework can be used to compute the pH-dependent membrane permeability for each of these two limiting treatments. With biased WTM-eABF molecular dynamics simulations, we computed the potential of mean force and diffusivity of each ionization state of two weakly basic small molecules: nicotine, an addictive drug, and varenicline, a therapeutic for treating nicotine addiction. At pH = 7, the BWAP effective permeability is greater than that determined by pH-partitioning by a factor of 2.5 for nicotine and 5 for varenicline. To assess the importance of ionization kinetics, we present a Smoluchowski master equation that includes explicitly the protonation and deprotonation processes coupled with the diffusive motion across the membrane. At pH = 7, the increase in permeability due to the explicit ionization kinetics is negligible for both nicotine and varenicline. This finding is reaffirmed by combined Brownian dynamics and Markov state model simulations for estimating the permeability of nicotine while allowing changes in its ionization state. We conclude that for these molecules the pH-partition hypothesis correctly captures the physics of the permeation process. The small free energy barriers for the permeation of nicotine and varenicline in their deprotonated neutral forms play a crucial role in establishing the validity of the pH-partitioning mechanism. Essentially, BWAP fails because ionization kinetics are too slow on the time scale of membrane crossing to affect the permeation of small ionizable molecules such as nicotine and varenicline. For the singly protonated state of nicotine, the computational results agree well with experimental measurements (P1 = 1.29 × 10-7 cm/s), but the agreement for neutral (P0 = 6.12 cm/s) and doubly protonated nicotine (P2 = 3.70 × 10-13 cm/s) is slightly worse, likely due to factors associated with the aqueous boundary layer (neutral form) or leaks through paracellular pathways (doubly protonated form).
Figures
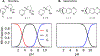
Similar articles
-
A mechanistic analysis to characterize oramucosal permeation properties.Int J Pharm. 1999 Jul 5;184(1):63-72. doi: 10.1016/s0378-5173(99)00091-5. Int J Pharm. 1999. PMID: 10425352
-
Dynamic Protonation Dramatically Affects the Membrane Permeability of Drug-like Molecules.J Am Chem Soc. 2019 Aug 28;141(34):13421-13433. doi: 10.1021/jacs.9b04387. Epub 2019 Aug 16. J Am Chem Soc. 2019. PMID: 31382734 Free PMC article.
-
How Azide Ion/Hydrazoic Acid Passes Through Biological Membranes: An Experimental and Computational Study.Protein J. 2023 Jun;42(3):229-238. doi: 10.1007/s10930-023-10127-3. Epub 2023 Jun 8. Protein J. 2023. PMID: 37289420 Free PMC article.
-
Physicochemical profiling (solubility, permeability and charge state).Curr Top Med Chem. 2001 Sep;1(4):277-351. doi: 10.2174/1568026013395100. Curr Top Med Chem. 2001. PMID: 11899112 Review.
-
Permeability of membranes to amino acids and modified amino acids: mechanisms involved in translocation.Amino Acids. 1994;6:213-29. Amino Acids. 1994. PMID: 11543596 Review.
Cited by
-
Statistical Mechanical Theories of Membrane Permeability.J Phys Chem B. 2024 Sep 26;128(38):9183-9196. doi: 10.1021/acs.jpcb.4c05020. Epub 2024 Sep 16. J Phys Chem B. 2024. PMID: 39283709 Free PMC article.
-
Computational Methods for Modeling Lipid-Mediated Active Pharmaceutical Ingredient Delivery.Mol Pharm. 2025 Mar 3;22(3):1110-1141. doi: 10.1021/acs.molpharmaceut.4c00744. Epub 2025 Jan 29. Mol Pharm. 2025. PMID: 39879096 Free PMC article. Review.
-
Scavenging acrolein with 2-HDP preserves neurovascular integrity in a rat model of diabetic retinal disease.Diabetologia. 2025 Aug 15. doi: 10.1007/s00125-025-06515-2. Online ahead of print. Diabetologia. 2025. PMID: 40815371
-
The Plasma Membrane may Serve as a Drug Depot to Drive the Extreme Potency of Fentanyl.bioRxiv [Preprint]. 2025 Jul 26:2025.07.22.666146. doi: 10.1101/2025.07.22.666146. bioRxiv. 2025. PMID: 40777490 Free PMC article. Preprint.
References
-
- Rashid M; Malik MY; Singh SK; Chaturvedi S; Gayen JR; Wahajuddin M Bioavailability enhancement of poorly soluble drugs: the holy grail in pharma industry. Current Pharmaceutical Design 2019, 25, 987–1020. - PubMed
-
- Tse CH; Comer J; Wang Y; Chipot C Link between membrane composition and permeability to drugs. J. Chem. Theory Comput 2018, 14, 2895–2909. - PubMed
-
- Loverde SM Molecular simulation of the transport of drugs across model membranes. The Journal of Physical Chemistry Letters 2014, 5, 1659–1665. - PubMed
-
- Oruç T; Küçük SE; Sezer D Lipid bilayer permeation of aliphatic amine and carboxylic acid drugs: rates of insertion, translocation and dissociation from MD simulations. Phys. Chem. Chem. Phys 2016, 18, 24511–24525. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

