Identifying the perceived local properties of networks reconstructed from biased random walks

Abstract

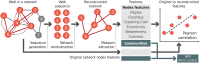
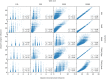
Many real-world systems give rise to a time series of symbols. The elements in a sequence can be generated by agents walking over a networked space so that whenever a node is visited the corresponding symbol is generated. In many situations the underlying network is hidden, and one aims to recover its original structure and/or properties. For example, when analyzing texts, the underlying network structure generating a particular sequence of words is not available. In this paper, we analyze whether one can recover the underlying local properties of networks generating sequences of symbols for different combinations of random walks and network topologies. We found that the reconstruction performance is influenced by the bias of the agent dynamics. When the walker is biased toward high-degree neighbors, the best performance was obtained for most of the network models and properties. Surprisingly, this same effect is not observed for the clustering coefficient and eccentric, even when large sequences are considered. We also found that the true self-avoiding displayed similar performance as the one preferring highly-connected nodes, with the advantage of yielding competitive performance to recover the clustering coefficient. Our results may have implications for the construction and interpretation of networks generated from sequences.

Fig 1. Example of a subgraph (highlighted in red) representing the limited information observed by a random walk starting at node A.

Fig 2. Schematics of the methodology.

First, we look into the original network and annotate the concerned properties for each node. In the next step, we iterate over the network with the desired dynamics in order to generate a sequence of symbols. In the third step, we reconstruct the network using the discovered nodes and edges, and we annotate the node’s properties in this reconstructed network. Finally, we build correlations among the reconstructed and original nodes by comparing each node i in the reconstructed network to its respective node in the original network.

Fig 3. Scatter-plot of node degree obtained in original vs. reconstructed LFR networks (with mixing parameter m = 0.05).

Each subpanel corresponds to a different configuration of agent dynamics and walks length (w). The walk length is distributed between 100 and 50,000 steps.

Fig 4. Evolution of the efficacy in recovering network metrics in reconstructed networks.

The x-axis represents the walk length used to generate the sequence, and the y-axis is the Pearson correlation for local metrics obtained in the original vs. reconstructed networks. The last columns are the NMI and ARI, which are used to compare the partitions in networks with community structure. While the coreness is not defined in BA and LFR networks, the NMI and ARI are computed only for networks with community structure.

Fig 5. Pearson correlation for the selected real networks.

Each data point represents the correlation of the same nodes for the original and reconstructed network from sequences acquired by dynamics for a given walk length, w (100 ≤ w ≤ 50000). The last columns represent the average NMI and ARI of each model obtained with the Leiden algorithm.

Fig 6. Efficiency in recovering network metrics in for the network models.

Each data point represents the correlation of local network metrics between the original and reconstructed network from sequences acquired by dynamics for a given walk length, where the x-axis represents the knowledge acquired for each walk length (w).

Fig 7. Pearson correlation for the selected real networks.

Each data point represents the correlation of the same nodes for the original and reconstructed network from sequences acquired by dynamics for a given walk length, where the x-axis represents the knowledge acquired for each walk length, w, where 100 ≤ w ≤ 50000.