Effect of Charge Distribution on the Dynamics of Polyampholytic Disordered Proteins

Abstract

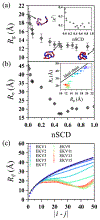
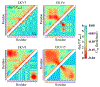
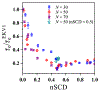
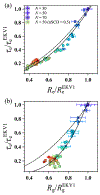
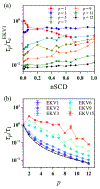
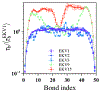
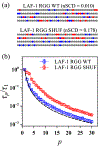
The stability and physiological function of many biomolecular coacervates depend on the structure and dynamics of intrinsically disordered proteins (IDPs) that typically contain a significant fraction of charged residues. Although the effect of relative arrangement of charged residues on IDP conformation is a well-studied problem, the associated changes in dynamics are far less understood. In this work, we systematically interrogate the effects of charge distribution on the chain-level and segmental dynamics of polyampholytic IDPs in dilute solutions. We study a coarse-grained model polyampholyte consisting of an equal fraction of two oppositely charged residues (glutamic acid and lysine) that undergoes a transition from an ideal chain-like conformation for uniformly charge-patterned sequences to a semi-compact conformation for highly charge-segregated sequences. Changes in the chain-level dynamics with increasing charge segregation correlate with changes in conformation. The chain-level and segmental dynamics conform to simple homopolymer models for uniformly charge-patterned sequences but deviate with increasing charge segregation, both in the presence and absence of hydrodynamic interactions. We discuss the significance of these findings, obtained for a model polyampholyte, in the context of a charge-rich intrinsically disordered region of the naturally occurring protein LAF-1. Our findings have important implications for understanding the effects of charge patterning on the dynamics of polyampholytic IDPs in dilute conditions using polymer scaling theories.

Figure 1:

Fifteen selected E–K variants (EKVs) for chain length $N=50$ with their identifying number and normalized SCD.

Figure 2:

(a) Radius of gyration $R_{\mathrm{g}}$ as a function of nSCD for the EKVs in Figure 1 along with representative conformations for select EKVs. The inset shows the relative anisotropy $⟨{\kappa }^2⟩$ as a function of nSCD for the same EKVs. (b) End-to-end distance $R_{\mathrm{e}}$ as a function of nSCD for the same EKVs. The inset shows the correlation between $R_{\mathrm{g}}$ and $R_{\mathrm{e}}$ from the simulations compared to the theoretical expectation for an ideal chain $R_{\mathrm{g}}=R_{\mathrm{e}}/\sqrt{6}$. (c) Interresidue distance $R_{ij}$ as a function of residue separation in the chain $|i-j|$ for select EKVs. The dashed line corresponds to the ideal chain scaling $R_{ij}=b|i-j{|}^{1/2}$, where $b=6.39\mathrm{\AA }$ was fitted for EKV1 using the theoretically expected end-to-end distance $R_{\mathrm{e}}^2=N{b}^2$ of an ideal chain with $N=50$. The symbol color, ranging from purple to red, indicates increasing nSCD. The same color scale is used in the inset of (b).

Figure 3:

Interresidue distance-based contact map $-\mathrm{l}\mathrm{n}\left(P/P_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$ (above diagonal) and energy map $U_{\mathrm{n}\mathrm{b}}$ (below diagonal) for select EKVs. The residue at each position is shown as a red (E) or blue (K) circle, respectively, on the axes. Two diagonals on either side of the main diagonal are removed in the maps to exclude directly bonded residues and residues that are separated by two bonds.

Figure 4:

Relaxation time ${\tau }_{\mathrm{e}}$ of the end-to-end vector, normalized by that of EKV1, as a function of nSCD for different chain lengths N.

Figure 5:

Relaxation time ${\tau }_{\mathrm{e}}$ of the end-to-end vector as a function of (a) end-to-end distance $R_{\mathrm{e}}$ and (b) radius of gyration $R_{\mathrm{g}}$. Data shown for different chain lengths N and for sequences shown in Figure S7, with all values normalized by those of EKV1 for each N. The solid lines in (a) and (b) correspond to power law fits ${\tau }_{\mathrm{e}}/{\tau }_{\mathrm{e}}^{\mathrm{E}\mathrm{K}\mathrm{V}1}=0.97{\left(R_{\mathrm{e}}/R_{\mathrm{e}}^{\mathrm{E}\mathrm{K}\mathrm{V}1}\right)}^{2.23}$ and ${\tau }_{\mathrm{e}}/{\tau }_{\mathrm{e}}^{\mathrm{E}\mathrm{K}\mathrm{V}1}=$ $1.04{\left(R_{\mathrm{g}}/R_{\mathrm{g}}^{\mathrm{E}\mathrm{K}\mathrm{V}1}\right)}^{3.66}$, respectively. The dashed lines in (a) and (b) correspond to the Rouse model scaling for an ideal chain with fixed number of segments N and varying segment size b, which gives ${\tau }_{\mathrm{e}}/{\tau }_{\mathrm{e}}^{\mathrm{E}\mathrm{K}\mathrm{V}1}={\left(R_{\mathrm{e}}/R_{\mathrm{e}}^{\mathrm{E}\mathrm{K}\mathrm{V}1}\right)}^2$ and ${\tau }_{\mathrm{e}}/{\tau }_{\mathrm{e}}^{\mathrm{E}\mathrm{K}\mathrm{V}1}={\left(R_{\mathrm{g}}/R_{\mathrm{g}}^{\mathrm{E}\mathrm{K}\mathrm{V}1}\right)}^2$. The symbol color, ranging from purple to red, indicates increasing nSCD.

Figure 6:

(a) Relaxation time ${\tau }_p$ of different normal modes, normalized by the end-to-end vector relaxation time of EKV1, as a function of nSCD for the EKVs. (b) Relaxation time ${\tau }_p$, normalized by that obtained for the $p=1$ mode, as a function of mode index p for select EKVs. The dashed line corresponds to the theoretically expected scaling of the Rouse model for an ideal chain.

Figure 7:

Relaxation time ${\tau }_{\mathrm{b}}$ of the bond vectors, normalized by the average relaxation time of all bonds in EKV1, as a function of bond index for select EKVs.

Figure 8:

(a) Amino acid sequences of LAF-1 RGG WT and its shuffled charge-segregated variant LAF-1 RGG SHUF, each of length $N=176$ residues. Negatively charged, positively charged, and uncharged residues are shown as red, blue, and gray circles, respectively. (b) Relaxation time ${\tau }_p$, normalized by that obtained for the $p=1$ mode, as a function of mode index p for LAF-1 RGG WT and LAF-1 RGG SHUF sequences. The dashed line corresponds to the theoretically expected scaling of the Rouse model for an ideal chain.

Figure 9:

Relaxation times of the (a) end-to-end vector ${\tau }_{\mathrm{e}}$, (b) normal modes ${\tau }_p$, and (c) bond vectors ${\tau }_{\mathrm{b}}$ for the model polyampholyte EKVs from the MPCD (+HI) and LD (−HI) simulations. (d) Relaxation time ${\tau }_p$ of the normal modes for LAF-1 RGG WT and LAF-1 RGG SHUF from the MPCD (+HI) simulations. All quantities are normalized as in Figures 4, 6, 7, and 8. The dashed lines in (b) and (d) are the expected scaling of the Zimm model for an ideal chain.