Generative modeling of biological shapes and images using a probabilistic α-shape sampler

Abstract

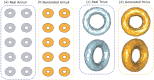
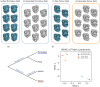
Understanding morphological variation is an important task in many areas of computational biology. Recent studies have focused on developing computational tools for the task of sub-image selection which aims at identifying structural features that best describe the variation between classes of shapes. A major part in assessing the utility of these approaches is to demonstrate their performance on both simulated and real datasets. However, when creating a model for shape statistics, real data can be difficult to access and the sample sizes for these data are often small due to them being expensive to collect. Meanwhile, the current landscape of generative models for shapes has been mostly limited to approaches that use black-box inference-making it difficult to systematically assess the power and calibration of sub-image models. In this paper, we introduce the $\alpha$-shape sampler: a probabilistic framework for generating realistic 2D and 3D shapes based on probability distributions which can be learned from real data. We demonstrate our framework using proof-of-concept examples and in two real applications in biology where we generate (i) 2D images of healthy and septic neutrophils and (ii) 3D computed tomography (CT) scans of primate mandibular molars. The $\alpha$-shape sampler R package is open-source and can be downloaded at https://github.com/lcrawlab/ashapesampler.

Figure 1.. An example of various α-shapes for the same set of points under different choices for the numerical parameter α.

Here, we consider different parameter values (a) $\alpha =0.05$, (b), $\alpha =0.10$, (c) $\alpha =0.15$, (d) $\alpha =0.2$, and (e) $\alpha =0.35$. In each panel, the gray shapes are the intersection of balls of radius $\alpha$ and the Voronoi cells at each point. The pink triangles are then faces representing the collective interior, and the blue lines are edges of the $\alpha$-complex. The bold blue edges are known as the “boundary edges” and denote the $\alpha$-shape for each panel. In (a) and (b), where $\alpha$ is smaller, we have disconnected components. In (c), we see an instance where edges may form the boundary of a face, but the face is not quite yet filled in since the three Voronoi cells have not collectively met. In (d), the faces are filled in and one of the points becomes an interior point while the rest remain $\alpha$-extreme points. In (e), $\alpha$ is large enough such that the given $\alpha$-complex is the Deluanay triangulation and convex hull of the point set. When determining how to generate a new shape from an existing dataset, we use information within the given simplicial complex to determine how many points are needed, where the points should be sampled, and the appropriate $\alpha$ parameter to connect the points. For a more detailed overview and theoretical discussion of concepts surrounding $\alpha$-shapes, see Materials and Methods and Supporting Information.

Figure 2.. Schematic overview of the α-shape sampler: a probabilistic framework for simulating realistic 2D and 3D images and shapes.

(a) A general illustration of the pre- and post-processing workflow in the $\alpha$-shape sampler software. In step (i), the user inputs data of real shapes in some format—in this case, binary masks for illustration. We refer to these data as “reference” shapes. In step (ii), the reference masks are converted to triangular meshes which are treated as simplicial complexes. In step (iii), the reference meshes are input into the shape generation pipeline which, in step (iv), outputs newly generated shapes in the form of $\alpha$-complexes. Finally, in step (v), these generated $\alpha$-complexes are converted back to match the same format as the original input data (again, here, binary masks). (b) Details underlying the algorithm for generating new shapes via the $\alpha$-shape sampler. (i) A collection meshes from $N$ reference shapes are given to the software. For simplicity, we assume that these shapes are from the same phenotypic class and, thus, their points are from the same manifold. (ii) Next, we estimate the reach ${\tau }_i$ for each reference shape by computing the distance to edge neighbors for each point (i.e., vertex in the mesh) and the circumcenters to neighboring faces (note that we also evaluate tetrahedra for 3D objects). The next closest vertex is the value ${\tau }_p$ for point $p$, and the smallest ${\tau }_p$ among all points is the value of ${\tau }_i$ for the $i$-th reference shape. We then take the minimum $\tau =({\tau }_1,\dots ,{\tau }_N)$ to be the representative estimate of the reach $\widehat{\tau }$ for all reference shapes. (iii) We create a partial point cloud by combining points from $J$ reference shapes in our input dataset, where $2\le J\le N$. Next, we sample new points from a ball of radius $\widehat{\tau }∕8$ around vertices in the partial point cloud. Each new point is accepted or rejected according to a probability-based rule. (iv) Once we have the newly sampled point cloud, we set $\alpha =\widehat{\tau }-ϵ$, where $ϵ>0$ is arbitrarily small, and generate the $\alpha$-complexes for new shapes.

Figure 3.. Qualitative comparisons of real and generated 2D annuli and 3D tori using the α-shape sampler.

Panels (a) and (b) show real (gray) and generated (orange) annuli. Similarly, in panels (c) and (d), we show real (gray) and generated (orange) tori. Overall, we see that the $\alpha$-shape sampler generates slightly thicker shapes than the examples in the original dataset (see Tables S1 and S2 for a quantitative evaluation). Nonetheless, the generated shapes preserve the most important topological property in that they all have exactly one connected component and exactly one hole.

Figure 4.. Application of the α-shape sampler to generate synthetic 2D images of healthy and septic neutrophils.

(a) Examples of real healthy (blue), generated healthy (light blue), real septic (black), and generated septic (gray) neutrophils in gels with stiffness 1.5 kilopascals (kPa). Each synthetic neutrophil in the second row was generated using the two shapes it sits in between in the row above. Variation in the newly generate cells can be most seen along the boundary, which is a function of the sampling process in the $\alpha$-shape pipeline. When comparing the generated and real cells, perhaps most noticeable are (i) the differences in area and (ii) the number of protrusions in the healthy versus septic cells. (b) We use a manifold regularized autoencoder (MRAE) to show that the generated shapes cluster and intermix with real cells in their respective categories. This provides evidence that the images being generated by the $\alpha$-shape sampler are realistic. (c) We compute the area, perimeter, circularity, solidity, convexity, and compactness of each real and generated cell. Next, we compare the distribution of these measurements for the healthy and septic groups, respectively. Here, if the $\alpha$-shape is able to preserve geometric and morphological characteristics while generating new data, then we would expect the distributions of these measurements to line up within a group. Note that due to the high heterogeneity and difficulty aligning shapes, the generated septic neutrophils are slightly larger in area and perimeter than the real ones. However, the generated neutrophils with the $\alpha$-shape sampler still capture other key shape characteristics.

Figure 5.. Application of the α-shape sampler to generate synthetic 3D primate mandibular molars.

Here, we qualitatively compare meshes of (a) real Microcebus, (b) generated Microcebus, (c) real Tarsius, and (d) generated Tarsius teeth. Morphologically, we know that tarsier teeth have an additional high cusp (highlighted in red) which allows this genus of primate to eat a wider range of foods. Here, we see that the generated Tarsius teeth from the $\alpha$-shape sampler preserve the unique paraconids. In panel (e), we show the phylogenetic relationship between the Microcebus and Tarsius genus. It has been estimated that the divergence dates of the Microcebus and Mirza from Tarsius happened around five million years before the branching of Tarsius from Saimiri. (f) We use a manifold regularized autoencoder (MRAE) to show that the generated teeth cluster and intermix with the real Microcebus and Tarsius teeth, respectively. Figure S4 shows that the same results hold regardless of the dimensionality reduction technique that is used.