The reproduction number and its probability distribution for stochastic viral dynamics
- PMID: 38264928
- PMCID: PMC10806437
- DOI: 10.1098/rsif.2023.0400
The reproduction number and its probability distribution for stochastic viral dynamics
Abstract
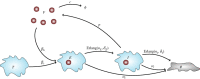
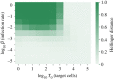
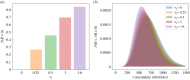
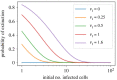
We consider stochastic models of individual infected cells. The reproduction number, R, is understood as a random variable representing the number of new cells infected by one initial infected cell in an otherwise susceptible (target cell) population. Variability in R results partly from heterogeneity in the viral burst size (the number of viral progeny generated from an infected cell during its lifetime), which depends on the distribution of cellular lifetimes and on the mechanism of virion release. We analyse viral dynamics models with an eclipse phase: the period of time after a cell is infected but before it is capable of releasing virions. The duration of the eclipse, or the subsequent infectious, phase is non-exponential, but composed of stages. We derive the probability distribution of the reproduction number for these viral dynamics models, and show it is a negative binomial distribution in the case of constant viral release from infectious cells, and under the assumption of an excess of target cells. In a deterministic model, the ultimate in-host establishment or extinction of the viral infection depends entirely on whether the mean reproduction number is greater than, or less than, one, respectively. Here, the probability of extinction is determined by the probability distribution of R, not simply its mean value. In particular, we show that in some cases the probability of infection is not an increasing function of the mean reproduction number.
Keywords: Erlang distribution; eclipse phase; infectious phase; reproduction number; stochastic model; viral burst size.
Conflict of interest statement
We declare we have no competing interests.
Figures



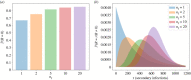
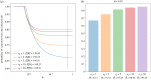
Similar articles
-
Stochastic models for virus and immune system dynamics.Math Biosci. 2011 Dec;234(2):84-94. doi: 10.1016/j.mbs.2011.08.007. Epub 2011 Sep 16. Math Biosci. 2011. PMID: 21945381 Free PMC article.
-
Stochastic theory of early viral infection: continuous versus burst production of virions.PLoS Comput Biol. 2011 Feb 3;7(2):e1001058. doi: 10.1371/journal.pcbi.1001058. PLoS Comput Biol. 2011. PMID: 21304934 Free PMC article.
-
A stochastic model for early HIV-1 population dynamics.J Theor Biol. 1998 Dec 21;195(4):451-63. doi: 10.1006/jtbi.1998.0806. J Theor Biol. 1998. PMID: 9837702
-
The effect of delay in viral production in within-host models during early infection.J Biol Dyn. 2019;13(sup1):47-73. doi: 10.1080/17513758.2018.1498984. Epub 2018 Jul 19. J Biol Dyn. 2019. PMID: 30021482
-
The stochastic dynamics of early epidemics: probability of establishment, initial growth rate, and infection cluster size at first detection.J R Soc Interface. 2021 Nov;18(184):20210575. doi: 10.1098/rsif.2021.0575. Epub 2021 Nov 17. J R Soc Interface. 2021. PMID: 34784776 Free PMC article. Review.
Cited by
-
Improved estimation of the effective reproduction number with heterogeneous transmission rates and reporting delays.Sci Rep. 2024 Nov 15;14(1):28125. doi: 10.1038/s41598-024-79442-8. Sci Rep. 2024. PMID: 39548195 Free PMC article.
-
Stochastic modelling of viral infection spread via a Partial Integro-Differential Equation.Infect Dis Model. 2025 Jul 7;10(4):1252-1269. doi: 10.1016/j.idm.2025.07.005. eCollection 2025 Dec. Infect Dis Model. 2025. PMID: 40689269 Free PMC article.
-
Apollo: A comprehensive GPU-powered within-host simulator for viral evolution and infection dynamics across population, tissue, and cell.bioRxiv [Preprint]. 2024 Oct 12:2024.10.07.617101. doi: 10.1101/2024.10.07.617101. bioRxiv. 2024. Update in: Nat Commun. 2025 Jul 1;16(1):5783. doi: 10.1038/s41467-025-60988-8. PMID: 39416208 Free PMC article. Updated. Preprint.
-
Apollo: a comprehensive GPU-powered within-host simulator for viral evolution and infection dynamics across population, tissue, and cell.Nat Commun. 2025 Jul 1;16(1):5783. doi: 10.1038/s41467-025-60988-8. Nat Commun. 2025. PMID: 40593638 Free PMC article.
-
Mathematical modelling of the role of Langerhans cells in the dynamics of HPV infection.Sci Rep. 2025 May 20;15(1):17505. doi: 10.1038/s41598-025-02608-5. Sci Rep. 2025. PMID: 40394091 Free PMC article.
References
Publication types
MeSH terms
Associated data
Grants and funding
LinkOut - more resources
Full Text Sources

