Measures of genetic diversification in somatic tissues at bulk and single-cell resolution
- PMID: 38265286
- PMCID: PMC10945735
- DOI: 10.7554/eLife.89780
Measures of genetic diversification in somatic tissues at bulk and single-cell resolution
Abstract
Intra-tissue genetic heterogeneity is universal to both healthy and cancerous tissues. It emerges from the stochastic accumulation of somatic mutations throughout development and homeostasis. By combining population genetics theory and genomic information, genetic heterogeneity can be exploited to infer tissue organization and dynamics in vivo. However, many basic quantities, for example the dynamics of tissue-specific stem cells remain difficult to quantify precisely. Here, we show that single-cell and bulk sequencing data inform on different aspects of the underlying stochastic processes. Bulk-derived variant allele frequency spectra (VAF) show transitions from growing to constant stem cell populations with age in samples of healthy esophagus epithelium. Single-cell mutational burden distributions allow a sample size independent measure of mutation and proliferation rates. Mutation rates in adult hematopietic stem cells are higher compared to inferences during development, suggesting additional proliferation-independent effects. Furthermore, single-cell derived VAF spectra contain information on the number of tissue-specific stem cells. In hematopiesis, we find approximately 2 × 105 HSCs, if all stem cells divide symmetrically. However, the single-cell mutational burden distribution is over-dispersed compared to a model of Poisson distributed random mutations. A time-associated model of mutation accumulation with a constant rate alone cannot generate such a pattern. At least one additional source of stochasticity would be needed. Possible candidates for these processes may be occasional bursts of stem cell divisions, potentially in response to injury, or non-constant mutation rates either through environmental exposures or cell-intrinsic variation.
Keywords: evolutionary biology; evolutionary inferences; healthy human tissues; human; sampling; single-cell mutation burden; stem cell dynamics; varient allele frequency.
© 2023, Moeller, Mon Père et al.
Conflict of interest statement
MM, NM, BW, WH No competing interests declared
Figures
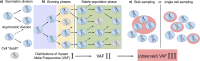





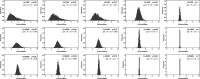


Update of
- doi: 10.1101/2022.11.07.515470
- doi: 10.7554/eLife.89780.1
- doi: 10.7554/eLife.89780.2
Comment in
- doi: 10.7554/eLife.95513
Similar articles
-
Capturing the unpredictability of stem cells.Elife. 2024 Mar 1;13:e95513. doi: 10.7554/eLife.95513. Elife. 2024. PMID: 38427029 Free PMC article.
-
Tissue-specific mutation accumulation in human adult stem cells during life.Nature. 2016 Oct 13;538(7624):260-264. doi: 10.1038/nature19768. Epub 2016 Oct 3. Nature. 2016. PMID: 27698416 Free PMC article.
-
Somatic mutation landscapes at single-molecule resolution.Nature. 2021 May;593(7859):405-410. doi: 10.1038/s41586-021-03477-4. Epub 2021 Apr 28. Nature. 2021. PMID: 33911282
-
A high-fidelity method for genomic sequencing of single somatic cells reveals a very high mutational burden.Exp Biol Med (Maywood). 2017 Jul;242(13):1318-1324. doi: 10.1177/1535370217717696. Exp Biol Med (Maywood). 2017. PMID: 28737476 Free PMC article. Review.
-
Strategies for homeostatic stem cell self-renewal in adult tissues.Cell. 2011 Jun 10;145(6):851-62. doi: 10.1016/j.cell.2011.05.033. Cell. 2011. PMID: 21663791 Review.
Cited by
-
Quantifying cell divisions along evolutionary lineages in cancer.Nat Genet. 2025 Mar;57(3):706-717. doi: 10.1038/s41588-025-02078-5. Epub 2025 Feb 4. Nat Genet. 2025. PMID: 39905260
-
On the patterns of genetic intra-tumor heterogeneity before and after treatment.Genetics. 2025 Aug 6;230(4):iyaf101. doi: 10.1093/genetics/iyaf101. Genetics. 2025. PMID: 40439127 Free PMC article.
-
Quantitative and sensitive sequencing of somatic mutations induced by a maize transposon.bioRxiv [Preprint]. 2025 Jun 10:2025.01.22.634239. doi: 10.1101/2025.01.22.634239. bioRxiv. 2025. Update in: Proc Natl Acad Sci U S A. 2025 Aug 12;122(32):e2426650122. doi: 10.1073/pnas.2426650122. PMID: 39896451 Free PMC article. Updated. Preprint.
-
cloneRate: fast estimation of single-cell clonal dynamics using coalescent theory.Bioinformatics. 2023 Sep 2;39(9):btad561. doi: 10.1093/bioinformatics/btad561. Bioinformatics. 2023. PMID: 37699006 Free PMC article.
-
Capturing the unpredictability of stem cells.Elife. 2024 Mar 1;13:e95513. doi: 10.7554/eLife.95513. Elife. 2024. PMID: 38427029 Free PMC article.
References
-
- Abascal F, Harvey LMR, Mitchell E, Lawson ARJ, Lensing SV, Ellis P, Russell AJC, Alcantara RE, Baez-Ortega A, Wang Y, Kwa EJ, Lee-Six H, Cagan A, Coorens THH, Chapman MS, Olafsson S, Leonard S, Jones D, Machado HE, Davies M, Øbro NF, Mahubani KT, Allinson K, Gerstung M, Saeb-Parsy K, Kent DG, Laurenti E, Stratton MR, Rahbari R, Campbell PJ, Osborne RJ, Martincorena I. Somatic mutation landscapes at single-molecule resolution. Nature. 2021;593:405–410. doi: 10.1038/s41586-021-03477-4. - DOI - PubMed
-
- Bailey C, Black JRM, Reading JL, Litchfield K, Turajlic S, McGranahan N, Jamal-Hanjani M, Swanton C. Tracking cancer evolution through the disease course. Cancer Discovery. 2021;11:916–932. doi: 10.1158/2159-8290.CD-20-1559. - DOI - PMC - PubMed
-
- Cagan A, Baez-Ortega A, Brzozowska N, Abascal F, Coorens THH, Sanders MA, Lawson ARJ, Harvey LMR, Bhosle S, Jones D, Alcantara RE, Butler TM, Hooks Y, Roberts K, Anderson E, Lunn S, Flach E, Spiro S, Januszczak I, Wrigglesworth E, Jenkins H, Dallas T, Masters N, Perkins MW, Deaville R, Druce M, Bogeska R, Milsom MD, Neumann B, Gorman F, Constantino-Casas F, Peachey L, Bochynska D, Smith ESJ, Gerstung M, Campbell PJ, Murchison EP, Stratton MR, Martincorena I. Somatic mutation rates scale with lifespan across mammals. Nature. 2022;604:517–524. doi: 10.1038/s41586-022-04618-z. - DOI - PMC - PubMed
-
- Caravagna G, Heide T, Williams MJ, Zapata L, Nichol D, Chkhaidze K, Cross W, Cresswell GD, Werner B, Acar A, Chesler L, Barnes CP, Sanguinetti G, Graham TA, Sottoriva A. Subclonal reconstruction of tumors by using machine learning and population genetics. Nature Genetics. 2020;52:898–907. doi: 10.1038/s41588-020-0675-5. - DOI - PMC - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

