Position-specific evolution in transcription factor binding sites, and a fast likelihood calculation for the F81 model
- PMID: 38269075
- PMCID: PMC10805598
- DOI: 10.1098/rsos.231088
Position-specific evolution in transcription factor binding sites, and a fast likelihood calculation for the F81 model
Abstract
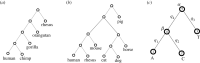
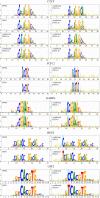
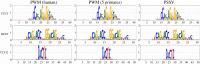
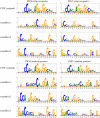
Transcription factor binding sites (TFBS), like other DNA sequence, evolve via mutation and selection relating to their function. Models of nucleotide evolution describe DNA evolution via single-nucleotide mutation. A stationary vector of such a model is the long-term distribution of nucleotides, unchanging under the model. Neutrally evolving sites may have uniform stationary vectors, but one expects that sites within a TFBS instead have stationary vectors reflective of the fitness of various nucleotides at those positions. We introduce 'position-specific stationary vectors' (PSSVs), the collection of stationary vectors at each site in a TFBS locus, analogous to the position weight matrix (PWM) commonly used to describe TFBS. We infer PSSVs for human TFs using two evolutionary models (Felsenstein 1981 and Hasegawa-Kishino-Yano 1985). We find that PSSVs reflect the nucleotide distribution from PWMs, but with reduced specificity. We infer ancestral nucleotide distributions at individual positions and calculate 'conditional PSSVs' conditioned on specific choices of majority ancestral nucleotide. We find that certain ancestral nucleotides exert a strong evolutionary pressure on neighbouring sequence while others have a negligible effect. Finally, we present a fast likelihood calculation for the F81 model on moderate-sized trees that makes this approach feasible for large-scale studies along these lines.
Keywords: compensatory mutation; evolution; transcription factor binding site.
© 2024 The Authors.
Conflict of interest statement
We declare we have no competing interests.
Figures



Similar articles
-
A general pairwise interaction model provides an accurate description of in vivo transcription factor binding sites.PLoS One. 2014 Jun 13;9(6):e99015. doi: 10.1371/journal.pone.0099015. eCollection 2014. PLoS One. 2014. PMID: 24926895 Free PMC article.
-
A DNA shape-based regulatory score improves position-weight matrix-based recognition of transcription factor binding sites.Bioinformatics. 2015 Nov 1;31(21):3445-50. doi: 10.1093/bioinformatics/btv391. Epub 2015 Jun 30. Bioinformatics. 2015. PMID: 26130577 Free PMC article.
-
A model of evolution with constant selective pressure for regulatory DNA sites.BMC Evol Biol. 2007 Jul 27;7:125. doi: 10.1186/1471-2148-7-125. BMC Evol Biol. 2007. PMID: 17662135 Free PMC article.
-
Dinucleotide weight matrices for predicting transcription factor binding sites: generalizing the position weight matrix.PLoS One. 2010 Mar 22;5(3):e9722. doi: 10.1371/journal.pone.0009722. PLoS One. 2010. PMID: 20339533 Free PMC article.
-
[Advances on bioinformatic research in transcription factor binding sites].Yi Chuan. 2009 Apr;31(4):365-73. doi: 10.3724/sp.j.1005.2009.00365. Yi Chuan. 2009. PMID: 19586888 Review. Chinese.
References
-
- Kulakovskiy IV, Levitsky VG, Oschepkov DG, Vorontsov IE, Makeev VJ. 2013. Learning advanced TFBS models from chip-seq data-diChIPMunk: effective construction of dinucleotide positional weight matrices. In Int. Conf. on Bioinformatics Models, Methods and Algorithms, vol. 2, pp. 146–150. Setúbal, Portugal: SciTePress, Science and Technology Publications.
LinkOut - more resources
Full Text Sources

