NON-UNIQUE GAMES OVER COMPACT GROUPS AND ORIENTATION ESTIMATION IN CRYO-EM
- PMID: 38274355
- PMCID: PMC10810340
- DOI: 10.1088/1361-6420/ab7d2c
NON-UNIQUE GAMES OVER COMPACT GROUPS AND ORIENTATION ESTIMATION IN CRYO-EM
Abstract
Let be a compact group and let . We define the Non-Unique Games (NUG) problem as finding to minimize . We introduce a convex relaxation of the NUG problem to a semidefinite program (SDP) by taking the Fourier transform of over . The NUG framework can be seen as a generalization of the little Grothendieck problem over the orthogonal group and the Unique Games problem and includes many practically relevant problems, such as the maximum likelihood estimator to registering bandlimited functions over the unit sphere in -dimensions and orientation estimation of noisy cryo-Electron Microscopy (cryo-EM) projection images. We implement a SDP solver for the NUG cryo-EM problem using the alternating direction method of multipliers (ADMM). Numerical study with synthetic datasets indicate that while our ADMM solver is slower than existing methods, it can estimate the rotations more accurately, especially at low signal-to-noise ratio (SNR).
Keywords: Computer vision; Primary: 00A69; Secondary: 90C34, 20C40; algorithms; cryo-EM; optimization; pattern recognition.
Figures

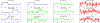


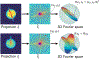
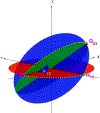
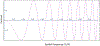

References
-
- Abbe E, Bandeira AS, Bracher A, and Singer A. Decoding binary node labels from censored edge measurements: Phase transition and efficient recovery. Network Science and Engineering, IEEE Transactions on, 1(1):10–22, Jan 2014.
-
- Abbe E, Bandeira AS, and Hall G. Exact recovery in the stochastic block model. IEEE Transactions on Information Theory, 62(1):471–487, 2016.
-
- Alon N and Naor A. Approximating the cut-norm via Grothendieck’s inequality. In Proc. of the 36 th ACM STOC, pages 72–80. ACM Press, 2004.
-
- Askey R. Orthogonal Polynomials and Special Functions. SIAM, 4 edition, 1975.
-
- ASPIRE - algorithms for single particle reconstruction software package. http://spr.math.princeton.edu/.
Grants and funding
LinkOut - more resources
Full Text Sources
