Visual guidance fine-tunes probing movements of an insect appendage

Abstract

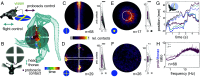
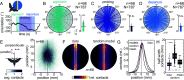
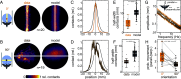
Visually guided reaching, a regular feature of human life, comprises an intricate neural control task. It includes identifying the target's position in 3D space, passing the representation to the motor system that controls the respective appendages, and adjusting ongoing movements using visual and proprioceptive feedback. Given the complexity of the neural control task, invertebrates, with their numerically constrained central nervous systems, are often considered incapable of this level of visuomotor guidance. Here, we provide mechanistic insights into visual appendage guidance in insects by studying the probing movements of the hummingbird hawkmoth's proboscis as they search for a flower's nectary. We show that visually guided proboscis movements fine-tune the coarse control provided by body movements in flight. By impairing the animals' view of their proboscis, we demonstrate that continuous visual feedback is required and actively sought out to guide this appendage. In doing so, we establish an insect model for the study of neural strategies underlying eye-appendage control in a simple nervous system.

Keywords: hawkmoth; insect; proboscis; visually guided reaching; visuomotor control.

Fig. 1.

Hawkmoths probe visual flower patterns with their proboscis. (A) Hawkmoths insert their long proboscis into the nectary of flowers while hovering in front of them. In principle, proboscis insertion requires guidance by flight maneuvers but might also involve active control of the proboscis. (B) To examine visuomotor control in this task, we analyzed both the moths’ body position in the air and proboscis movements on the flower using high-speed video tracking of the head, thorax, and proboscis tip during flower probing. (C–F) Proboscis contacts on artificial flower patterns (symbols depict pattern types), normalized and averaged across individuals (n). The Insets for line and cross patterns and the pattern-less condition show the number of proboscis contacts ±2 mm off the pattern axes, compared to the same area rotated 90° or 45°, respectively (see symbols below the graph). For the circle pattern, the number of contacts on the pattern was compared to those on the background, normalized by the respective areas. Statistical comparisons were performed using Wilcoxon signed-rank tests (SI Appendix, Table S1). Their results are abbreviated as * (P < 0.05), ** (P < 0.01), *** (P < 0.001), and n.s. (not significant). (G) Example of the trajectory of the thorax (dark blue), head (light blue), and proboscis (purple), and (H) ratio of the amplitude spectrum of proboscis and thorax movements during flower probing (SI Appendix, Fig. S3).

Fig. 2.

Hawkmoths used flight control to coarsely position their proboscis on flower patterns. (A) The hawkmoths’ head-to-thorax body orientation relative to the pattern orientation in three different stages of flower interaction: the approach 250 ms immediately before proboscis contact (turquoise), the departure 250 ms immediately after the last proboscis contact (blue), and the probing time in between (dark blue). (B–D) The animals’ orientation during the approach, probing, and departure. Each line represents a probing trial (N) of one animal (n). The Inset bar graphs depict the results of a statistical test (GLMM with binomial distribution, see Materials and Methods, SI Appendix, Table S2) to assess whether the hawkmoths’ body orientation fell into the pattern sectors (white background) significantly more frequently than chance. Depicted are the mean and CI of the probability of body orientations within pattern sectors, as well as the prediction for random orientations (black line). (E) To generate a prediction of the hawkmoths’ proboscis positions based on passive movement by the body in flight, the proboscis positions relative to the body were extracted for each video frame. (F) Relative proboscis positions were then randomly assigned to a body position for each frame of a probing trial video (as in Fig. 1C, data). Ten iterations of this random assignment were generated for each trial of each animal (model). (G) The relative number of contacts summed along the pattern axis for the data and random model, as well as a model based on the mean proboscis position of each animal. Shown are the mean and SEM. (H) Half-width of the contact distribution depicted in (G) for all flower probing trials (N) of all animals (n). A Mann–Whitney rank-sum test was used for statistical comparison of the data and random model (N = 787, z-score = −11.86, P < 0.001) and a signed-rank test for the paired data and mean model (z-score = −2.62, P = 0.009). Statistical results are abbreviated as * (P < 0.05), ** (P < 0.01), *** (P < 0.001), and n.s. (not significant).

Fig. 3.

Hawkmoths used visually guided proboscis movements to fine-tune their probing. (A and B) To isolate the hawkmoths’ proboscis movements from their flight maneuvers, a corridor surrounding the artificial flowers confined the moths’ head–thorax axis parallel to the corridor axis. Orienting the pattern axis parallel (A, 0°) or perpendicular (B, 90°) to the corridor required the animals to perform proboscis movements with more parallel or perpendicular components relative to their body axis for optimal pattern probing. Normalized contact distributions (data, Left panels) and a prediction of random proboscis placement (model, Right panels, see Materials and Methods and Fig. 2 E and F) are shown for both conditions. (C and D) The relative number of contacts summed along the pattern axis for the data (brown hues) and model (gray). Shown are the mean and SEM. (E and F) Half-width of the contact distribution depicted in (C and D) for all flower probing trials of all animals (n). A Mann–Whitney rank-sum test was used for statistical comparison (n_data = 20, n_model = 200, z-score = −6.76 and n_data = 19, n_model = 190, z-score = −6.07). (G) The amplitude of proboscis movements parallel (dashed) and perpendicular (solid) to the body orientation in the 0° (orange) and 90° (brown) conditions. Their ratio is depicted in (H). Statistical comparison was performed using a Wilcoxon signed-rank test (n₀ = 20, n₉₀ = 19, z-score = −11.86, P = 0.003). All statistical results are abbreviated as * (P < 0.05), ** (P < 0.01), *** (P < 0.001), and n.s. (not significant).

Fig. 4.

Visual feedback is required for proboscis targeting. (A) To obstruct the hawkmoths’ view of their proboscis during probing, their fronto-visual field was occluded in both eyes by applying black paint. Normalized contact densities of the control condition with free eyes (Left), and with occluded visual field (Right). (B) Ratio of proboscis contacts on the pattern (dark shaded Inset) versus the respective 90° rotated area (light shaded Inset) for the free and occluded treatment. Contacts scored in the outer thirds (Left) and in the central third (Right) of the pattern. Statistical comparisons were performed using Wilcoxon signed-rank tests (SI Appendix, Table S3). (C) The mean vector of the hawkmoths’ proboscis tracks for all animals (n) and flower approaches (N) with free and occluded frontal visual fields. Pattern sectors are in white, background sectors in gray. The Inset bar graphs depict the results of a statistical test (GLMM with binomial distribution, see Materials and Methods, SI Appendix, Table S4) to assess whether the mean probing direction aligned with the pattern sectors. Depicted are the mean and CI of this probability, as well as the prediction for random orientations (black line). (D) Proboscis probing positions with either the right or left frontal visual field occluded. (E) Distribution of proboscis contacts (mean and SEM) summed along the pattern axis for animals with left (light green) and right (dark green) occlusion. The Lower panel shows the position of the median of the contact distribution for all trials. Statistical analysis comparing the median probing positions was performed by a Mann–Whitney rank-sum test. A Wilcoxon signed-rank test was used to compare the median positions to the pattern axis midline (SI Appendix, Table S3). (F) Mean vector of the proboscis probing tracks for all trials with left and right occlusion. The statistical results are depicted as in (C) and abbreviated as * < 0.05, ** < 0.01, *** < 0.001, and n.s. not significant.