HyperMinHash: MinHash in LogLog space

Abstract

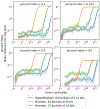
In this extended abstract, we describe and analyze a lossy compression of MinHash from buckets of size $O\left(logn\right)$ to buckets of size $O\left(loglogn\right)$ by encoding using floating-point notation. This new compressed sketch, which we call HyperMinHash, as we build off a HyperLogLog scaffold, can be used as a drop-in replacement of MinHash. Unlike comparable Jaccard index fingerprinting algorithms in sub-logarithmic space (such as b-bit MinHash), HyperMinHash retains MinHash's features of streaming updates, unions, and cardinality estimation. For an additive approximation error $ϵ$ on a Jaccard index $t$, given a random oracle, HyperMinHash needs $O\left({ϵ}^{-2}(loglogn+log\frac{1}{ϵ}\right))$ space. HyperMinHash allows estimating Jaccard indices of 0.01 for set cardinalities on the order of ${10}^{19}$ with relative error of around 10% using 2MiB of memory; MinHash can only estimate Jaccard indices for cardinalities of ${10}^{10}$ with the same memory consumption.

Keywords: compression; hyperloglog; min-wise hashing; sketching; streaming.

Fig. 1.

HyperMinHash generates sketches in the same fashion as one-permutation k-partition MinHash, but stores the hashes in floating-point notation. It begins by hashing each object in the set to a uniform random number between 0 and 1 , encoded in binary. Then, the hashed values are partitioned by the first $p$ bits (above, 2 bits, in green), and the minimum value within each partition is taken. For ordinary MinHash, the procedure stops here, and a fixed number of bits (above, 64 bits) after the first $p$ bits are taken as the hash value. For HyperMinHash, each value is further lossily compressed as an exponent (blue) and a mantissa (red); the exponent is the position of the leftmost 1 bit in the next $2^q$ bits, and $2^q+1$ otherwise (above, $q=6$). The mantissa is simply the value of the next $r$ bits in the bit-string (above, $r=4$).

Fig. 2.

HyperLogLog sections, used alone, result in collisions whenever the minimum hashes match in order of magnitude.

Fig. 3.

HyperMinHash further subdivides HyperLogLog leading 1indicator buckets, achieving a much smaller collision space, so long as we precisely store the position of the leading 1.

Fig. 4.

In practice, HyperMinHash has a limited number of bits for the LogLog counters, so there is a final lower left bucket at the precision limit.

Fig. 5.

We will upper bound the collision probability of HyperMinHash by dividing it into these four regions of integration: (a) the Top Right orange box, (b), the magenta ray covering intermediate boxes, (c) the black strip covering all but the final purple box, and (d) the final purple sub-bucket by the origin.

Fig. 6.. For a fixed size sketch, HyperMinHash has better accuracy and/or cardinality range than MinHash.

We compare Jaccard index estimation for identically sized sets with Jaccard index of 0.1, 1/3, 0.5, and 0.9, and plot the mean relative errors without estimated collision correction. All datasets represent between 8 and 96 random repetitions, as needed to get reasonable 95% confidence interval (shaded bands). (blue) A 64 byte HyperMinHash sketch, with 64 buckets of 8 bits each, 4 bits of which are allocated to the LogLog counter. Jaccard index estimation remains stable until cardinalities around $2^{21}$. (orange) A 64 byte MinHash sketch with 64 buckets of 8 bits each achieves similar accuracy at low cardinalities, but fails once cardinalities approach $2^{13}$. (green) A 64 byte MinHash sketch with 32 buckets of 16 bits can access larger cardinalities of around $2^{19}$, but to do so trades off on low-cardinality accuracy.