Ranked Subtree Prune and Regraft
- PMID: 38294587
- PMCID: PMC10830682
- DOI: 10.1007/s11538-023-01244-2
Ranked Subtree Prune and Regraft
Abstract
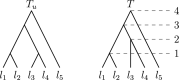
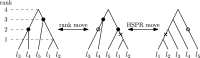
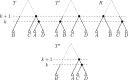
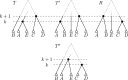
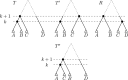
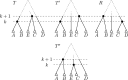
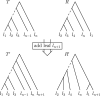
Phylogenetic trees are a mathematical formalisation of evolutionary histories between organisms, species, genes, cancer cells, etc. For many applications, e.g. when analysing virus transmission trees or cancer evolution, (phylogenetic) time trees are of interest, where branch lengths represent times. Computational methods for reconstructing time trees from (typically molecular) sequence data, for example Bayesian phylogenetic inference using Markov Chain Monte Carlo (MCMC) methods, rely on algorithms that sample the treespace. They employ tree rearrangement operations such as [Formula: see text] (Subtree Prune and Regraft) and [Formula: see text] (Nearest Neighbour Interchange) or, in the case of time tree inference, versions of these that take times of internal nodes into account. While the classic [Formula: see text] tree rearrangement is well-studied, its variants for time trees are less understood, limiting comparative analysis for time tree methods. In this paper we consider a modification of the classical [Formula: see text] rearrangement on the space of ranked phylogenetic trees, which are trees equipped with a ranking of all internal nodes. This modification results in two novel treespaces, which we propose to study. We begin this study by discussing algorithmic properties of these treespaces, focusing on those relating to the complexity of computing distances under the ranked [Formula: see text] operations as well as similarities and differences to known tree rearrangement based treespaces. Surprisingly, we show the counterintuitive result that adding leaves to trees can actually decrease their ranked [Formula: see text] distance, which may have an impact on the results of time tree sampling algorithms given uncertain "rogue taxa".
Keywords: Phylogenetics; Ranked trees; Time trees; Tree Rearrangements; Tree distance; Treespace.
© 2024. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures
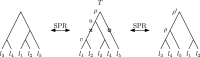
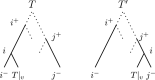
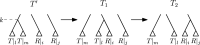
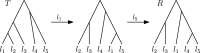

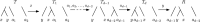
Similar articles
-
Computing nearest neighbour interchange distances between ranked phylogenetic trees.J Math Biol. 2021 Jan 25;82(1-2):8. doi: 10.1007/s00285-021-01567-5. J Math Biol. 2021. PMID: 33492606 Free PMC article.
-
Neighborhoods of trees in circular orderings.Bull Math Biol. 2015 Jan;77(1):46-70. doi: 10.1007/s11538-014-0049-1. Epub 2014 Dec 5. Bull Math Biol. 2015. PMID: 25477080
-
Discrete coalescent trees.J Math Biol. 2021 Nov 5;83(5):60. doi: 10.1007/s00285-021-01685-0. J Math Biol. 2021. PMID: 34739608 Free PMC article.
-
Review Paper: The Shape of Phylogenetic Treespace.Syst Biol. 2017 Jan 1;66(1):e83-e94. doi: 10.1093/sysbio/syw025. Syst Biol. 2017. PMID: 28173538 Free PMC article. Review.
-
Comparison of phylogenetic trees defined on different but mutually overlapping sets of taxa: A review.Ecol Evol. 2024 Aug 8;14(8):e70054. doi: 10.1002/ece3.70054. eCollection 2024 Aug. Ecol Evol. 2024. PMID: 39119174 Free PMC article. Review.
Cited by
-
The Number and Pattern of Viral Genomic Reassortments are not Necessarily Identifiable from Segment Trees.Mol Biol Evol. 2024 Jun 1;41(6):msae078. doi: 10.1093/molbev/msae078. Mol Biol Evol. 2024. PMID: 38648521 Free PMC article.
References
-
- Allen BL, Steel M. Subtree transfer operations and their induced metrics on evolutionary trees. Ann Comb. 2001;5(1):1–15. doi: 10.1007/s00026-001-8006-8. - DOI
-
- Atkins R, McDiarmid C. Extremal distances for subtree transfer operations in binary trees. Ann Comb. 2019;23(1):1–26. doi: 10.1007/s00026-018-0410-4. - DOI
-
- Bordewich M, Semple C. On the computational complexity of the rooted subtree prune and regraft distance. Ann Comb. 2005;8(4):409–423. doi: 10.1007/s00026-004-0229-z. - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

