Information representation in an oscillating neural field model modulated by working memory signals

Abstract

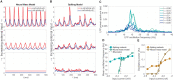
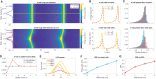
We study how stimulus information can be represented in the dynamical signatures of an oscillatory model of neural activity-a model whose activity can be modulated by input akin to signals involved in working memory (WM). We developed a neural field model, tuned near an oscillatory instability, in which the WM-like input can modulate the frequency and amplitude of the oscillation. Our neural field model has a spatial-like domain in which an input that preferentially targets a point-a stimulus feature-on the domain will induce feature-specific activity changes. These feature-specific activity changes affect both the mean rate of spikes and the relative timing of spiking activity to the global field oscillation-the phase of the spiking activity. From these two dynamical signatures, we define both a spike rate code and an oscillatory phase code. We assess the performance of these two codes to discriminate stimulus features using an information-theoretic analysis. We show that global WM input modulations can enhance phase code discrimination while simultaneously reducing rate code discrimination. Moreover, we find that the phase code performance is roughly two orders of magnitude larger than that of the rate code defined for the same model solutions. The results of our model have applications to sensory areas of the brain, to which prefrontal areas send inputs reflecting the content of WM. These WM inputs to sensory areas have been established to induce oscillatory changes similar to our model. Our model results suggest a mechanism by which WM signals may enhance sensory information represented in oscillatory activity beyond the comparatively weak representations based on the mean rate activity.

Keywords: computational model; information theory; neural coding; phase; working memory.

Figure 1

An unstable equilibrium, in which oscillations emerge, occurs in a protruding region in I-σ parameter space. (A) F-I curve solutions f_σ(I) to Eqs. (4–6), parameterized by the diffusion noise σ parameter. (B) Increasing σ reduces the overall firing rate gain at a given firing rate df_σ/dI|_fσ. (C) The real part of the smallest-magnitude eigenvalue Re(λ_k) parameterized by the input I (abscissa), and F-I curve gain parameter σ (ordinate). There is a subregion where the eigenvalues are complex ω = Im(λ_k) ≠ 0, in which crossing into the instability region produces a supercritical Hopf bifurcation (magenta dashed line). (D) Moving from left to right and from low, to high, the mean firing rate increases in a continuous manner, both outside and inside the unstable region. (E) Inside the unstable region, the oscillation frequency increases going diagonally up and to the right. (F) The supercritical Hopf bifurcation elicits oscillation amplitudes that emerge continuously from zero on the upper part of the unstable region. In (D–F) the brown line from left to right indicates a input parameter path of interest where oscillations emerge via supercritical Hopf in which mean firing rate, oscillation frequency, and weak amplitude oscillations increase continuously from zero.

Figure 2

The emergence of oscillations through increased input in the neural mass model corresponds similar emergent oscillations in the large-N LIF spiking network model from which the neural mass model was derived. (A) Sample solution trajectories of the neural mass model at three ascending input levels (I = −2.45, −2.3, −2.15) one below the bifurcation (lower panel), one just slightly above (middle), and one further beyond (top). (B) The large-N (N_e, N_i = 20, 000) LIF spiking network driven at the same inputs and parameter settings as the neural mass model in (A). (C) The power spectrum of the large-N LIF model over seven input levels (four more levels interleaved between the three illustrated in (A, B) shows that increasing input I produces greater oscillatory power, and a shift toward higher frequencies within the β-oscillatory band. (D, E) The mean oscillation frequency and oscillatory power, respectively, computed from the power spectra in (C) for the LIF spiking network, and the neural mass model.

Figure 3

The neural field model replicates oscillatory behaviors observed in sensory areas during WM tasks. (A) The neural field e-cell oscillatory dynamics over its feature space in the presence of no stimulus (top), depicted along with the weight kernel 𝒲 (top left sub panel; see Eq. 11). In the presence of a stimulus 𝒮 (bottom, left sub panel red curve; see Eq. 12), the e-cells exhibit an oscillation with a bend located at the stimulus location. Two example stimulus feature locations θ = π/2, π/4 are shown on the ring in the top panel, yellow, red-dash, respectively. Neural field model example simulations exhibit phase locked oscillations across the ring, but preferred stimulus exhibits earlier activity. (B) e-cell firing rate on ring at the two example locations over 100ms simulation time for increasing stimulus contrast from no-stimulus (top) and with-stimulus (bottom). (C) The associated spike phase distributions for the same two example stimulus features as in (B) in no-stimulus and with-stimulus (top and bottom). (D) The difference in spike count distributions between the two example stimulus features in no-stimulus and with-stimulus conditions shows weak (~ 10⁻³) average spike count changes due to stimulus, while peak firing rate during an oscillatory cycle exhibits 3Hz differences between stimuli [see (B), bottom]. (E–G) Increases in WM input produce LFP peak power and LFP frequency increases, mean firing rate increases, and increased in SPL, respectively.

Figure 4

Divergent sensory discrimination performance is exhibited by the phase and rate codes as a function of WM input. (A) IG measure shows enhancement for the phase code across all non-zero stimulus contrasts while the rate code is reduced, measured on a log ordinate scale. Insets of (A) The same data as the main panel but plotted on a ordinate linear scale as a function of contrast, which shows increasing WM input enhances the coding gain as a function of contrast while reducing rate coding gain for the same WM increases. (B) Qualitatively similar results to (A) but for the MI coding performance measure. All error bars reflect standard deviations.