Completing the picture of field-grown cereal crops: a new method for detailed leaf surface models in wheat

Abstract

Background: The leaf angle distribution (LAD) is an important structural parameter of agricultural crops that influences light interception, radiation fluxes and consequently plant performance. Therefore, LAD and its parametrized form, the Beta distribution, is used in many photosynthesis models. However, in field cultivations, these parameters are difficult to assess and cereal crops in particular pose challenges since their leaves are thin, flexible, and often bent and twisted around their own axis. To our knowledge, there is only a very limited set of methods currently available to calculate LADs of field-grown cereal crops that explicitly takes these special morphological properties into account.

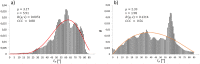
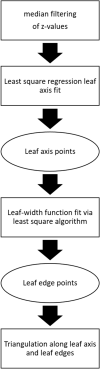
Results: In this study, a new processing pipeline is introduced that allows for the generation of realistic leaf surface models and the analysis of LADs of field-grown cereal crops from 3D point clouds. The data acquisition is based on a convenient stereo imaging setup. The approach was validated with different artificial targets and results on the accuracy of the 3D reconstruction, leaf surface modeling and calculated LAD are given. The mean error of the 3D reconstruction was below 1 mm for an inclination angle range between 0° and 75° and the leaf surface could be quantified with an average accuracy of 90%. The concordance correlation coefficient (CCC) of 99.6% (p-value = [Formula: see text]) indicated a high correlation between the reconstructed inclination angle and the identity line. The LADs for bent leaves were reconstructed with a mean error of 0.21° and a standard deviation of 1.55°. As an additional parameter, the insertion angle was reconstructed for the artificial leaf model with an average error < 5°. Finally, the method was tested with images of field-grown cereal crops and Beta functions were approximated from the calculated LADs. The mean CCC between reconstructed LAD and calculated Beta function was 0.66. According to Cohen, this indicates a high correlation.

Conclusion: This study shows that our image processing pipeline can reconstruct the complex leaf shape of cereal crops from stereo images. The high accuracy of the approach was demonstrated with several validation experiments including artificial leaf targets. The derived leaf models were used to calculate LADs for artificial leaves and naturally grown cereal crops. This helps to better understand the influence of the canopy structure on light absorption and plant performance and allows for a more precise parametrization of photosynthesis models via the derived Beta distributions.

Keywords: 3D plant reconstruction; Beta distribution; Cereal crops; Leaf angle; Leaf angle distribution; Plant phenotyping; Stereo imaging; Structural leaf model.

Fig. 1

Relation between reconstructed inclination angle $i_r$ and manually measured inclination angle ${\alpha }_m$. The red line marks the identity line. All points are located very close to the identity line (red) indicating a high accuracy of the reconstructed inclination angle

Fig. 2

Reconstructed inclination angle along the leaf axis. Plot a shows the inclination angle $i_c$ (Ref) and $i_r$ (Rec) along the leaf axis $X$. Plot b shows the difference between $i_c$ and $i_r$. The difference between $i_r$ and $i_c$ $\mathrm{\Delta }\left(i_c,,,i_r\right)$ varies between − 6° and 4°. Mean error (ME) and standard deviation σ for $\mathrm{\Delta }(i_c,i_r)$ for the four reconstructions (Rec_n) were: Rec₁: ME = − 0.43°, σ = 2.38; Rec₂: ME = 0.37°, σ = 1.22°; Rec₃: ME = 0.73°, σ = 0.68; Rec₄: ME = 0.51, σ = 1.05

Fig. 3

Reconstructed leaf angle distribution and mean error of reconstructed leaf angles. a Calculated leaf angle distribution ${\theta }_c$ (red) versus reconstructed leaf angle distribution ${\theta }_r$ (black). Systematic differences only occurred for inclination angles close to 0°. b Mean error (black) and standard deviation (grey area) between the calculated leaf angle distribution ${\theta }_c$ and reconstructed distribution ${\theta }_r$. The mean error is close to 0° for inclination angles between 10° and 60°. For horizontal surfaces with an inclination angle close to 0°, $e_r$ shows the highest value of ~ 2°

Fig. 4

Leaf reconstruction for field grown wheat plants. The stereo image (master camera) shows individual leaves, and the plots show different views of the respective reconstructed 3D point clouds and leaf fits (modeled edges and axis in black)

Fig. 5

Common errors of leaf reconstructions for field grown wheat plants. The image shows a stereo image (master camera) with three selected leaves. The 3D point clouds show three different views of the respective reconstructed leaf fits (modeled edges and axis in black) and a visualization of the reconstructed leaf inclination angle projected on the leaf model. Leaf a is uniformly twisted around the leaf axis (red arrow iv)). This twisting is visible in the corresponding reconstructions. Leaf b is partly occluded (red arrow i)) by another leaf. For this reason, the 3D-point cloud is fragmented into two parts. However, the leaf model interpolates the missing areas. Moreover, leaf b is tilted laterally due to local twisting and axis bending. Therefore, the reconstructed leaf edges do not fit the border of the 3D-point cloud over the entire leaf length. The leaf axis position in the image (red arrow iii)) differs from the leaf axis fit position (green arrow iii)). Leaf c as a slanted leaf surface. For this reason, the point cloud does not contain the leaf tip

Fig. 6

Leaf angle distribution modelled by Beta function. Analysis of two reconstructed field-grown wheat canopies that shows the reconstructed leaf angle distributions θ (black bars) and calculated Beta functions with $f\left(t\right)=\frac{1}{B\left(\mu ,\text{,},\nu \right)}\ast {\left(1,-,t\right)}^{\mu -1}\ast t^{\nu -1}$ (a) red; (b) orange), both displaying a high concordance (CCC > 0.5) between distribution and fit; a) CCC = 0.8, and b) CCC = 0.56 (Variety: Matthus; sowing density: $250\frac{\mathit{seeds}}{m^2})$

Fig. 7

Experimental setup. a The stereo-setup was mounted in nadir position to the imaging object. b Stereo-setup with two AV Prosilica GT3400C cameras and 35 mm lenses. c Artificial plant model composed of a node module and a bent leaf

Fig. 8

Artificial plant model. a The node module fixes the leaf module with a defined inclination angle. The leaf is plugged in a small socket in the module center. The socket inclination is changed by a screw and determines the inclination angle of the fixed leaf (left). The spacer module is used to vary the distance between leaves. They are available in heights (h) of 20 mm, 40 mm and 50 mm (right). Lateral view on b planar and c bent artificial leaves. The insertion angle α describes the initial inclination angle at the stem. Parameter r denotes the leaf bending radius

Fig. 9

Flow chart of the leaf modeling process. Before leaf fitting, a cluster-wise median filtering of $\mathrm{p}\prime$ was applied

Fig. 10

Detailed visualization of the leaf fitting process from points cloud to mathematical leaf model