Rapid exchange cooling with trapped ions
- PMID: 38316766
- PMCID: PMC11258264
- DOI: 10.1038/s41467-024-45232-z
Rapid exchange cooling with trapped ions
Abstract
The trapped-ion quantum charge-coupled device (QCCD) architecture is a leading candidate for advanced quantum information processing. In current QCCD implementations, imperfect ion transport and anomalous heating can excite ion motion during a calculation. To counteract this, intermediate cooling is necessary to maintain high-fidelity gate performance. Cooling the computational ions sympathetically with ions of another species, a commonly employed strategy, creates a significant runtime bottleneck. Here, we demonstrate a different approach we call exchange cooling. Unlike sympathetic cooling, exchange cooling does not require trapping two different atomic species. The protocol introduces a bank of "coolant" ions which are repeatedly laser cooled. A computational ion can then be cooled by transporting a coolant ion into its proximity. We test this concept experimentally with two 40Ca+ ions, executing the necessary transport in 107 μs, an order of magnitude faster than typical sympathetic cooling durations. We remove over 96%, and as many as 102(5) quanta, of axial motional energy from the computational ion. We verify that re-cooling the coolant ion does not decohere the computational ion. This approach validates the feasibility of a single-species QCCD processor, capable of fast quantum simulation and computation.
© 2024. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures

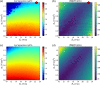
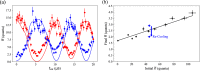




References
-
- Moses SA, et al. A Race-Track Trapped-Ion Quantum Processor. Phys. Rev. X. 2023;13:041052.
LinkOut - more resources
Full Text Sources
Miscellaneous

