The probability of edge existence due to node degree: a baseline for network-based predictions

Abstract

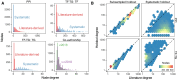
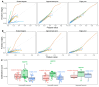
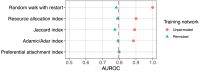
Important tasks in biomedical discovery such as predicting gene functions, gene-disease associations, and drug repurposing opportunities are often framed as network edge prediction. The number of edges connecting to a node, termed degree, can vary greatly across nodes in real biomedical networks, and the distribution of degrees varies between networks. If degree strongly influences edge prediction, then imbalance or bias in the distribution of degrees could lead to nonspecific or misleading predictions. We introduce a network permutation framework to quantify the effects of node degree on edge prediction. Our framework decomposes performance into the proportions attributable to degree and the network's specific connections using network permutation to generate features that depend only on degree. We discover that performance attributable to factors other than degree is often only a small portion of overall performance. Researchers seeking to predict new or missing edges in biological networks should use our permutation approach to obtain a baseline for performance that may be nonspecific because of degree. We released our methods as an open-source Python package (https://github.com/hetio/xswap/).

Keywords: Python; XSwap; bioinformatics; edge prediction; edge prior; heterogeneous; knowledge graphs; networks; node degree; permutation.

Figure 1:

Biomedical networks are characterized by nonuniform degree distributions. Eight degree distributions are plotted for 6 edge types, Hetionet v1.0 [5]. Hetionet integrates subnetworks for 24 different edge types, the degree distributions of which are analyzed separately. Furthermore, bipartite (e.g., Anatomy→expresses→Gene) and directed (e.g., Gene→regulates→Gene) graphs (Hetionet edge types) have both source and target degrees that must be assessed separately. Undirected edge types (e.g., Compound–resembles–Compound) have only a single degree distribution. Degree distributions are nonuniform and vary greatly between different networks. The y-axis is log₁₀-scaled to accommodate the common occurrence where most nodes have low degree while a small portion of nodes have high degree. Several distributions have nodes that reach the maximum degree, corresponding to a node being connected to all other possible nodes. Zero-degree nodes are not displayed, since methodological limitations often result in edge data only existing for a subset of nodes.

Figure 2:

XSwap algorithm pseudocode. (A) XSwap algorithm presented by Hanhijärvi et al. [15]. (B) Extension of the XSwap algorithm to other types of networks.

Figure 3:

Modified XSwap algorithm graphical explanation.

Figure 4:

The XSwap-derived edge prior can be analytically approximated. The analytical approximation is plotted against the XSwap-derived edge prior for 3 networks (edge types) from Hetionet. The strong correlation suggests that the approximation will be suitable for applications where computation time is a limiting factor.

Figure 5:

(A) Degree distributions of networks with and without degree bias can be very different. Data on PPI and TF-TG were split between literature-derived and systematically derived networks. In both cases, the networks exhibit large differences in degree distribution. Coauthorship relationship networks split by date of first coauthorship roughly share their degree distributions. (B) Comparison of individual node degrees between different networks. Not only are the overall degree distributions different, but individual nodes can have systematically different degrees between 2 networks. Uniform random sampling produces linearly correlated node degree, while nonrandom sampling produces noncorrelated degree. Systematically derived networks are not uniformly sampled from literature-derived networks or vice versa. Seventy percent of literature edges were sampled with uniform probability for the “Subsampled holdout” network.

Figure 6:

The edge prior accurately assigns the probability of edge existence. (A) Calibration curves for full network reconstruction of 20 networks from Hetionet. For every unique predictor value on the horizontal axis, the fraction of node pairs with that predictor value having an edge in the network is shown on the vertical axis. The permutation-based edge prior’s calibration was superior to the other 2 strategies based on degree. (B) Calibration curves for sampled network reconstruction. The edge prior shows superior calibration in the 20 Hetionet networks. (C) Individual Hetionet edge-type calibration estimated by the 2-component decomposition of the Brier score, in which lower scores indicate better calibration. The edge prior has excellent calibration in unsampled and sampled networks, and each considered method is sensitive to shifts in the degree distribution.

Figure 7:

Degree can predict edges within a given network but does not generalize to networks with different degree distributions. The edge prior is able to reconstruct the networks on which it was computed (task 1, “unsampled,” 20 different networks) with high performance. When computed on a sampled network, the edge prior can reconstruct the unsampled network with slightly lower performance (task 2, “sampled,” 20 different networks). However, when computed on a completely different network (having a different degree distribution) of the same type of data, the edge prior’s performance is greatly reduced (task 3, “separate,” 3 different networks). The performance reduction from computing predictors on sampled networks is real but far smaller compared to a new degree distribution. This indicates that while degree can be effective for network reconstruction, it is far less effective in predicting edges from a different degree distribution.

Figure 8:

Common edge prediction metrics correlate with node degree. Five common edge prediction features (Supplementary Table S2) are correlated with node degree on the STRING PPI network [24]. All 5 features show a positive relationship with degree, although the magnitude of this correlation is highly variable. The preferential attachment index is understandably perfectly correlated because it is equal to the product of source and target degree. Each panel indicates the Pearson correlation (“r”) between feature and degree in the lower right corner.

Figure 9:

Identifying the fraction of a metric’s performance resulting from degree alone. Network reconstruction performances by 5 edge prediction features. Dotted red line indicates performance of the edge prior. Each feature was computed on both the unpermuted and 100 permutations of the STRING PPI network.