Climate-invariant machine learning
- PMID: 38324696
- PMCID: PMC10849594
- DOI: 10.1126/sciadv.adj7250
Climate-invariant machine learning
Abstract
Projecting climate change is a generalization problem: We extrapolate the recent past using physical models across past, present, and future climates. Current climate models require representations of processes that occur at scales smaller than model grid size, which have been the main source of model projection uncertainty. Recent machine learning (ML) algorithms hold promise to improve such process representations but tend to extrapolate poorly to climate regimes that they were not trained on. To get the best of the physical and statistical worlds, we propose a framework, termed "climate-invariant" ML, incorporating knowledge of climate processes into ML algorithms, and show that it can maintain high offline accuracy across a wide range of climate conditions and configurations in three distinct atmospheric models. Our results suggest that explicitly incorporating physical knowledge into data-driven models of Earth system processes can improve their consistency, data efficiency, and generalizability across climate regimes.
Figures

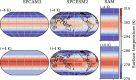
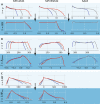




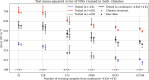

References
-
- Reichstein M., Camps-Valls G., Stevens B., Jung M., Denzler J., Carvalhais N., Prabhat, Deep learning and process understanding for data-driven Earth system science. Nature 566, 195–204 (2019). - PubMed
-
- T. Beucler, I. Ebert-Uphoff, S. Rasp, M. Pritchard, P. Gentine, “Machine learning for clouds and climate” in Clouds and their Climatic Impacts: Radiation, Circulation, and Precipitation (John Wiley & Sons, 2023), pp. 325–345.
-
- Irrgang C., Boers N., Sonnewald M., Barnes E. A., Kadow C., Staneva J., Saynisch-Wagner J., Towards neural Earth system modelling by integrating artificial intelligence in Earth system science. Nat. Mach. Intell. 3, 667–674 (2021).
-
- de Burgh-Day C. O., Leeuwenburg T., Machine learning for numerical weather and climate modelling: A review. Geosci. Model Dev. 16, 6433–6477 (2023).
-
- Molina M. J., O’Brien T. A., Anderson G., Ashfaq M., Bennett K. E., Collins W. D., Dagon K., Restrepo J. M., Ullrich P. A., A review of recent and emerging machine learning applications for climate variability and weather phenomena. Artif. Intell. Earth Syst. 2, 220086 (2023).
LinkOut - more resources
Full Text Sources
Miscellaneous

