Biaxial Structures of Localized Deformations and Line-like Distortions in Effectively 2D Nematic Films

Abstract

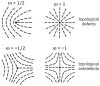
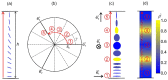
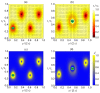
We numerically studied localized elastic distortions in curved, effectively two-dimensional nematic shells. We used a mesoscopic Landau-de Gennes-type approach, in which the orientational order is theoretically considered by introducing the appropriate tensor nematic order parameter, while the three-dimensional shell shape is described by the curvature tensor. We limited our theoretical consideration to axially symmetric shapes of nematic shells. It was shown that in the surface regions of stomatocyte-class nematic shell shapes with large enough magnitudes of extrinsic (deviatoric) curvature, the direction of the in-plane orientational ordering can be mutually perpendicular above and below the narrow neck region. We demonstrate that such line-like nematic distortion configurations may run along the parallels (i.e., along the circular lines of constant latitude) located in the narrow neck regions of stomatocyte-like nematic shells. It was shown that nematic distortions are enabled by the order reconstruction mechanism. We propose that the regions of nematic shells that are strongly elastically deformed, i.e., topological defects and line-like distortions, may attract appropriately surface-decorated nanoparticles (NPs), which could potentially be useful for the controlled assembly of NPs.

Keywords: nematic shells; order reconstruction mechanism; orientational order; stomatocytes; topological defects.

Figure 1

Typical topological defects and their charges in two dimensions.

Figure 2

Schematic presentation of the order reconstruction (OR) mechanism. (a) System subjected to conflicting boundary condition at $z=0$ and $z=h$. The imposed frustration could be realized via the OR mechanism (b–d), where representative states of the transformation are labeled with the numbers 1 to 5. Due to topological reasons, the negative uniaxial state along ${\overrightarrow{e}}_2$ must be realized in between (b–d). Furthermore, this state takes place between the two regions exhibiting maximal biaxiality (${\beta }^2=1$) (c,d).

Figure 3

Orientational ordering configuration and the degree of biaxiality on a spherical shell. (a) The amplitude of nematic order $s/s_0$ (presented with color coding) and the orientation of molecules (denoted by the rods) in the $(\phi ,l)$-plane. (b) 3D visualization of the equilibrium texture of the amplitude of nematic order $s/s_0$. The degree of biaxiality ${\beta }^2$ presented as a 3D plot (c) and with color coding (d). $L_s$ stands for the length of the shape profile curve. The parameters used in the simulations are $R/\xi =5$, $k_e=k_i/2$, $q_3=0.04$.

Figure 4

Orientational ordering configuration and the degree of biaxiality on a stomatocyte vesicle shape. (a) The amplitude of nematic order $s/s_0$ (presented with color coding) and the orientation of molecules (denoted by the rods) in the $(\phi ,l)$-plane. (b) Equilibrium texture of the amplitude of nematic order $s/s_0$ plotted on half of the stomatocyte shape. The degree of biaxiality ${\beta }^2$ presented as a 3D plot (c) and with color coding (d). $L_s$ stands for the length of the shape profile curve. The parameters used in the simulations are $R/\xi =7$, $k_e=k_i/2$, $q_3=0.04$.

Figure 5

Orientational ordering configuration (a,b) and the degree of biaxiality (c,d) on a spherical nematic shell with a nanoparticle represented as a green circle with the inscribed “NP”. The NP–LC interaction is characterized by $\mu \ll 1$ in (a,c) and by $\mu \gg 1$ in (b,d). The amplitude of nematic order $s/s_0$ is presented with color coding, while the orientation of molecules is denoted by the rods in the $(\phi ,l)$-plane (a,b). The degree of biaxiality ${\beta }^2$ is presented with color coding (c,d). $L_s$ stands for the length of the shape profile curve. The parameters used in the simulations are $R/\xi =3.5$, $k_e=k_i/2$, $q_3=0.04$.

Figure 6

Schematic representation of the endocytosis process in biological membranes, illustrating cross-sections of the membrane around the particle in different phases of particle engulfment. Panel (a) shows a free particle (drawn in red) in the vicinity of the membrane (drawn in black). Panel (b) shows the initial stage of particle engulfment by the membrane, and panel (c) illustrates the progressive engulfment driven by particle-membrane adhesion/binding forces [67] and the non-homogeneous distribution of membrane constituents [3]. At the end of the engulfment process, a thin membrane neck is formed, as schematically shown in panel (d), which may then disappear in the process of fission [68], where the membrane-enveloped particle is detached from the membrane (see panel (e)).