This is a preprint.
Metapopulation model of phage therapy of an acute Pseudomonas aeruginosa lung infection
- PMID: 38352502
- PMCID: PMC10862780
- DOI: 10.1101/2024.01.31.578251
Metapopulation model of phage therapy of an acute Pseudomonas aeruginosa lung infection
Update in
-
Metapopulation model of phage therapy of an acute Pseudomonas aeruginosa lung infection.mSystems. 2024 Oct 22;9(10):e0017124. doi: 10.1128/msystems.00171-24. Epub 2024 Sep 4. mSystems. 2024. PMID: 39230264 Free PMC article.
Abstract
Infections caused by multi-drug resistant (MDR) pathogenic bacteria are a global health threat. Phage therapy, which uses phage to kill bacterial pathogens, is increasingly used to treat patients infected by MDR bacteria. However, the therapeutic outcome of phage therapy may be limited by the emergence of phage resistance during treatment and/or by physical constraints that impede phage-bacteria interactions in vivo. In this work, we evaluate the role of lung spatial structure on the efficacy of phage therapy for Pseudomonas aeruginosa infection. To do so, we developed a spatially structured metapopulation network model based on the geometry of the bronchial tree, and included the emergence of phage-resistant bacterial mutants and host innate immune responses. We model the ecological interactions between bacteria, phage, and the host innate immune system at the airway (node) level. The model predicts the synergistic elimination of a P. aeruginosa infection due to the combined effects of phage and neutrophils given sufficiently active immune states and suitable phage life history traits. Moreover, the metapopulation model simulations predict that local MDR pathogens are cleared faster at distal nodes of the bronchial tree. Notably, image analysis of lung tissue time series from wild-type and lymphocyte-depleted mice (n=13) revealed a concordant, statistically significant pattern: infection intensity cleared in the bottom before the top of the lungs. Overall, the combined use of simulations and image analysis of in vivo experiments further supports the use of phage therapy for treating acute lung infections caused by P. aeruginosa while highlighting potential limits to therapy given a spatially structured environment, such as impaired innate immune responses and low phage efficacy.
Figures
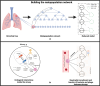
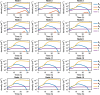



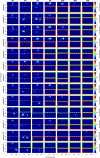
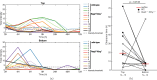
References
-
- World Health Organization et al., “2021 antibacterial agents in clinical and preclinical development: an overview and analysis,” World Health Organization, 2022.
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
