Aggregation and structural phase transitions of semiflexible polymer bundles: A braided circuit topology approach

Abstract

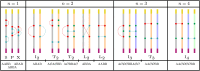
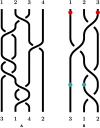
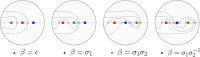
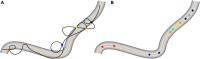
We present a braided circuit topology framework for investigating topology and structural phase transitions in aggregates of semiflexible polymers. In the conventional approach to circuit topology, which specifically applies to single isolated folded linear chains, the number and arrangement of contacts within the circuitry of a folded chain give rise to increasingly complex fold topologies. Another avenue for achieving complexity is through the interaction and entanglement of two or more folded linear chains. The braided circuit topology approach describes the topology of such multiple-chain systems and offers topological measures such as writhe, complexity, braid length, and isotopy class. This extension of circuit topology to multichains reveals the interplay between collapse, aggregation, and entanglement. In this work, we show that circuit topological motif fractions are ideally suited order parameters to characterize structural phase transitions in entangled systems that can detect structural re-ordering other measures cannot.

Keywords: Interdisciplinary physics; polymers.

Graphical abstract

Figure 1

The set of circuit topology motifs for $n=1,2,3,4$ strands Contacts A and B are indicated by red and turquoise filled circles, respectively, while ghost contacts $\mathcal{O}$ are indicated by filled green circles. Different chains are indicated by different colors. The colored chain ends indicate the orientation of the strands; we choose to orient every strand from the yellow to the violet end. Corresponding string notations are given below each motif, where the string is read in n-tuples.

Figure 2

Braid diagrams with the braid index n indicated, showing the permutations (A) A braid with $n=4$ with string notation ${\mathcal{S}}_4={\sigma }_2{\sigma }_1^{-1}{\sigma }_3^{-1}{\sigma }_1{\sigma }_1{\sigma }_2{\sigma }_2^{-1}$. (B) A braid containing contacts $A,B$ indicated by red and turquoise points, respectively. The string notation is ${\mathcal{S}}_3=A\mathcal{O}A{\sigma }_2^{-1}{\sigma }_1^{-1}{\sigma }_{2}BB\mathcal{O}{\sigma }_2$.

Figure 3

The punctured disk representation of the braid complexity for four different braids (A‒D) Braid string notations. Punctures corresponding to strands are indicated by colored dots. The operators ${\sigma }_i,{\sigma }_i^{-1}$ change punctures i and $i+1$ CW or CCW, respectively. Intersections with the central axis are indicated by open circles.

Figure 4

The steps involved in primitive path analysis (A) The reduction of a fluctuating polymer (black line) within its confining tube (gray) to a primitive path (orange line). Hard contacts are indicated by colored points. (B) Topological arrangement of the individual hard contact points (colored) within the polymer’s primitive path.

Figure 5

Density plots of the topological observables for $N=10$ as a function of the stiffness κ It can be easily seen that there is a transition from an amorphous to an aligned aggregate around $\kappa \approx 7$. The colors indicate the probability of an observable having a value given on the y axis. For high stiffness values, all observables stabilise around a fixed distribution.

Figure 6

Observables in the polymer system with $M=4$, $N=10$ at $T=1$, $\rho =0.01$ (A) Writhe W, complexity C and length L. (B) The rescaled radius of gyration ${\tilde{R}}_g$ and correlation parameter $C_R$. (C) Circuit topology fractions of the different motifs; error bars are smaller than symbol size. (D) Isotopy class given by the TN types (RE, FO, PA), and representative structural conformations of the system at different κ. All results are averaged over 1000 runs. Error bars indicate one standard deviation on the mean values.

Figure 7

Observables in the polymer system with $M=4$, $N=30$ at $T=0.1$, $\rho =0.01$ (A) Writhe W, complexity C and length L. (B) The rescaled radius of gyration ${\tilde{R}}_g$ and correlation parameter $C_R$. (C) Circuit topology fractions of the different motifs; error bars are smaller than symbol size. All results are averaged over 1000 runs. Error bars indicate one standard deviation on the mean values.

Figure 8

Density plots of the topological observables for $N=30$ as a function of the stiffness κ It can be easily seen that there is a transition from an amorphous to an aligned aggregate around $\kappa \approx 8$. The colors indicate the probability of an observable having a value given on the y axis. For high stiffness values, all observables stabilise around a fixed distribution.