Bloch oscillations, Landau-Zener transition, and topological phase evolution in an array of coupled pendula

Abstract

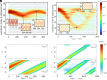
We experimentally and theoretically study the dynamics of a one-dimensional array of pendula with a mild spatial gradient in their self-frequency and where neighboring pendula are connected with weak and alternating coupling. We map their dynamics to the topological Su-Schrieffer-Heeger model of charged quantum particles on a lattice with alternating hopping rates in an external electric field. By directly tracking the dynamics of a wave-packet in the bulk of the lattice, we observe Bloch oscillations, Landau-Zener transitions, and coupling between the isospin (i.e., the inner wave function distribution within the unit cell) and the spatial degrees of freedom (the distribution between unit cells). We then use Bloch oscillations in the bulk to directly measure the nontrivial global topological phase winding and local geometric phase of the band. We measure an overall evolution of 3.1 [Formula: see text] 0.2 radians for the geometrical phase during the Bloch period, consistent with the expected Zak phase of [Formula: see text]. Our results demonstrate the power of classical analogs of quantum models to directly observe the topological properties of the band structure and shed light on the similarities and the differences between quantum and classical topological effects.

Keywords: Bloch oscillations; Landau–Zener transition; metamaterials; topological phase.

Fig. 1.

(A) Sketch of the mechanical system: pendula coupled to each other by knots (depicted by red and blue dots) connecting adjacent strings at varying and alternating heights ${\delta }_{j,j+1}$. The pendulum lengths $r_j$ have a mild gradient according to Eq. 1. (B) The experiment started with a wave pattern implemented using a board that was cut according to the desired wave-packet. Then the board was abruptly removed and the pendula started to evolve freely. (C) The solution to Eq. 7 in Fourier space, exhibiting Bloch oscillations due to the external field: The initial wave packet (black) travels toward negative $k$ values and follows the SSH lower energy band (blue). Then at $k=-\pi$, depending on the parameters of Eq. 7, the wave continues its travel either adiabatically following the lower band, or by jumping through LZ diabatic transition and following the upper band (red), or by following in a superposition of the two bands.

Fig. 2.

(A and B) The pendulum displacements in Experiments 1 (A) and 3 (B). Each line shows a pendulum displacement as a function of time and is shifted vertically according to the pendulum index. Bloch oscillations are clearly seen in both experiments. In Experiment 1, the wave follows adiabatically the lower band, while in Experiment 3 after one Bloch period, the system is in a superposition of waves in the Lower and Upper bands. The Insets show zoom-ins of the pendulum displacements at certain times, in which the state of the partial wave (its mean $k$ value, and the band) can be identified (see text); (C and D) Discrete spatial Fourier transform of the pendulum motion at each time, projected onto the two theoretical eigenstates of the SSH problem, Eq. 11. These represent the partial wave in the Lower (Bottom) and Upper (Top) bands.

Fig. 3.

(A) The simulated rate of Bloch oscillations compared with the theoretical prediction $\frac{\mathit{dk}}{d\tau }=\sqrt{\frac{g}{r}}\alpha$ for a significant range of the values of the parameters $g$, $r$, and $\alpha$. The solid line marks the identity. The experimentally measured value (red) of the Bloch period agrees with the theoretical prediction, with the error-bar marking the spread between Experiments 1, 2, and 3. (B) The LZ diabatic transition probability as extracted from experiments and simulations, Eq. 13, vs. the theoretical prediction, Eq. 12. The simulations covered variations in all parameters, $g$, $r$, $\kappa$, ${\kappa }^{\prime }$, and $\alpha$. The solid line marks the identity. Inset: relative deviation of the simulated values from the prediction. For reasonable values of $ϵ=\sqrt{r(\kappa +{\kappa }^{\prime })/gm}$, which control the accuracy of the mapping of the array of pendula to the SSH model, the deviation is 5% or less.

Fig. 4.

(A) Phase difference between the dimer components, $arg\left(u_{b,k(\tau )}\right)-arg\left(u_{a,k(\tau )}\right)$ at $k(\tau )=-Ea\tau$, as extracted from the displacements of the pendula in Experiments 1 (dark green line) and 2 (blue line). The dashed red lines show the theoretical curves $arg(\kappa +{\kappa }^{\prime }{e}^{iEa\tau })$, where in Experiment 1, $\kappa =0.0035$ N/m,${\kappa }^{\prime }=0.07$ N/m and in Experiment 2, $\kappa =0.07$ N/m, ${\kappa }^{\prime }=0.035$ N/m. The accuracy of the couplings is about $5\%$ (1 mm in the knots’ heights). The purple dotted line marks the Bloch oscillation period $T_B$. The winding number of the phase after a full Bloch oscillation clearly shows that in Experiment 1 the set-up was in the non-trivial topological phase, while in Experiment 2 it was in the trivial topological phase. (B) Difference in global phase evolution of $u_{a,-eE\tau }$ between Experiments 2 and 1, where the full phase evolution from the two experiments are shown in the Inset. After 700 s, and about 2,500 radians of phase evolution of the swings of the pendula, the difference between the phases reached $\pi$ to very good accuracy. The dashed red line is the theoretical prediction $\frac{1}{2}arg({\kappa }^{\prime }+\kappa e^{-iEa\tau })-\frac{1}{2}arg(\kappa +{\kappa }^{\prime }{e}^{-iEa\tau })$, with $\kappa =0.035$ N/m, ${\kappa }^{\prime }=0.07$ N/m.