Efficiency and resilience of cooperation in asymmetric social dilemmas
- PMID: 38408249
- PMCID: PMC10927524
- DOI: 10.1073/pnas.2315558121
Efficiency and resilience of cooperation in asymmetric social dilemmas
Abstract
Direct reciprocity is a powerful mechanism for cooperation in social dilemmas. The very logic of reciprocity, however, seems to require that individuals are symmetric, and that everyone has the same means to influence each others' payoffs. Yet in many applications, individuals are asymmetric. Herein, we study the effect of asymmetry in linear public good games. Individuals may differ in their endowments (their ability to contribute to a public good) and in their productivities (how effective their contributions are). Given the individuals' productivities, we ask which allocation of endowments is optimal for cooperation. To this end, we consider two notions of optimality. The first notion focuses on the resilience of cooperation. The respective endowment distribution ensures that full cooperation is feasible even under the most adverse conditions. The second notion focuses on efficiency. The corresponding endowment distribution maximizes group welfare. Using analytical methods, we fully characterize these two endowment distributions. This analysis reveals that both optimality notions favor some endowment inequality: More productive players ought to get higher endowments. Yet the two notions disagree on how unequal endowments are supposed to be. A focus on resilience results in less inequality. With additional simulations, we show that the optimal endowment allocation needs to account for both the resilience and the efficiency of cooperation.
Keywords: direct reciprocity; evolution of cooperation; inequality; public good games; social dilemmas.
Conflict of interest statement
Competing interests statement:The authors declare no competing interest.
Figures
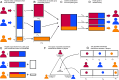
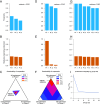
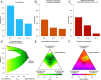

Similar articles
-
Social dilemmas among unequals.Nature. 2019 Aug;572(7770):524-527. doi: 10.1038/s41586-019-1488-5. Epub 2019 Aug 15. Nature. 2019. PMID: 31413366
-
Cooperation and coordination in heterogeneous populations.Philos Trans R Soc Lond B Biol Sci. 2023 May 8;378(1876):20210504. doi: 10.1098/rstb.2021.0504. Epub 2023 Mar 20. Philos Trans R Soc Lond B Biol Sci. 2023. PMID: 36934745 Free PMC article.
-
Cooperation among unequal players with aspiration-driven learning.J R Soc Interface. 2024 Mar;21(212):20230723. doi: 10.1098/rsif.2023.0723. Epub 2024 Mar 13. J R Soc Interface. 2024. PMID: 38471536 Free PMC article.
-
Universal scaling for the dilemma strength in evolutionary games.Phys Life Rev. 2015 Sep;14:1-30. doi: 10.1016/j.plrev.2015.04.033. Epub 2015 May 5. Phys Life Rev. 2015. PMID: 25979121 Review.
-
Reputation and reciprocity.Phys Life Rev. 2023 Sep;46:8-45. doi: 10.1016/j.plrev.2023.05.002. Epub 2023 May 10. Phys Life Rev. 2023. PMID: 37244154 Review.
References
-
- Kerr B., Godfrey-Smith P., Feldman M. W., What is altruism? Trends Ecol. Evol. 19, 135–140 (2004). - PubMed
-
- Nowak M. A., et al. , Evolving cooperation. J. Theor. Biol. 299, 1–8 (2012). - PubMed
-
- Trivers R., The evolution of reciprocal altruism. Q. Rev. Biol. 46, 35–57 (1971).
-
- Axelrod R., The emergence of cooperation among egoists. Am. Polit. Sci. Rev. 75, 306–318 (1981).
MeSH terms
LinkOut - more resources
Full Text Sources

