Tracing curves in the plane: Geometric-invariant learning from human demonstrations
- PMID: 38416741
- PMCID: PMC10901316
- DOI: 10.1371/journal.pone.0294046
Tracing curves in the plane: Geometric-invariant learning from human demonstrations
Abstract
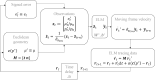
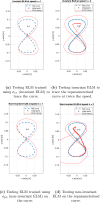
The empirical laws governing human-curvilinear movements have been studied using various relationships, including minimum jerk, the 2/3 power law, and the piecewise power law. These laws quantify the speed-curvature relationships of human movements during curve tracing using critical speed and curvature as regressors. In this work, we provide a reservoir computing-based framework that can learn and reproduce human-like movements. Specifically, the geometric invariance of the observations, i.e., lateral distance from the closest point on the curve, instantaneous velocity, and curvature, when viewed from the moving frame of reference, are exploited to train the reservoir system. The artificially produced movements are evaluated using the power law to assess whether they are indistinguishable from their human counterparts. The generalisation capabilities of the trained reservoir to curves that have not been used during training are also shown.
Copyright: © 2024 Turlapati et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
One of the authors (DC) holds equity positions in ARTICARES Pte. Ltd., a company that manufactures robotic devices for rehabilitation similar to the device used in this study. This does not alter our adherence to PLOS ONE policies on sharing data and materials.
Figures

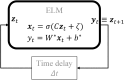





Similar articles
-
Affine differential geometry analysis of human arm movements.Biol Cybern. 2007 Jun;96(6):577-601. doi: 10.1007/s00422-007-0145-5. Epub 2007 Apr 4. Biol Cybern. 2007. PMID: 17406889 Free PMC article.
-
The speed-curvature power law of movements: a reappraisal.Exp Brain Res. 2018 Jan;236(1):69-82. doi: 10.1007/s00221-017-5108-z. Epub 2017 Oct 25. Exp Brain Res. 2018. PMID: 29071361
-
Spectrum of power laws for curved hand movements.Proc Natl Acad Sci U S A. 2015 Jul 21;112(29):E3950-8. doi: 10.1073/pnas.1510208112. Epub 2015 Jul 6. Proc Natl Acad Sci U S A. 2015. PMID: 26150514 Free PMC article.
-
Timing of continuous motor imagery: the two-thirds power law originates in trajectory planning.J Neurophysiol. 2015 Apr 1;113(7):2490-9. doi: 10.1152/jn.00421.2014. Epub 2015 Jan 21. J Neurophysiol. 2015. PMID: 25609105 Free PMC article.
-
Biological kinematics: a detailed review of the velocity-curvature power law calculation.Exp Brain Res. 2025 Apr 3;243(5):107. doi: 10.1007/s00221-025-07065-0. Exp Brain Res. 2025. PMID: 40178611 Free PMC article. Review.
References
-
- Mündermann Lars, Corazza Stefano, and Andriacchi Thomas P. “The evolution of methods for the capture of human movement leading to markerless motion capture for biomechanical applications.” Journal of neuroengineering and rehabilitation 3, no. 1 (2006): 1–11. doi: 10.1186/1743-0003-3-6 - DOI - PMC - PubMed
-
- Rosenbaum David A. Human motor control. Academic press, 2009.
-
- Shadmehr Reza, and Mussa-Ivaldi Sandro. Biological learning and control: how the brain builds representations, predicts events, and makes decisions. Mit Press, 2012.
MeSH terms
LinkOut - more resources
Full Text Sources

