Microstructure reconstruction of 2D/3D random materials via diffusion-based deep generative models
- PMID: 38424207
- PMCID: PMC10904791
- DOI: 10.1038/s41598-024-54861-9
Microstructure reconstruction of 2D/3D random materials via diffusion-based deep generative models
Abstract
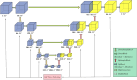
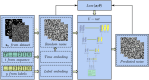
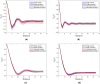
Microstructure reconstruction serves as a crucial foundation for establishing process-structure-property (PSP) relationship in material design. Confronting the limitations of variational autoencoder and generative adversarial network within generative models, this study adopted the denoising diffusion probabilistic model (DDPM) to learn the probability distribution of high-dimensional raw data and successfully reconstructed the microstructures of various composite materials, such as inclusion materials, spinodal decomposition materials, chessboard materials, fractal noise materials, and so on. The quality of generated microstructure was evaluated using quantitative measures like spatial correlation functions and Fourier descriptor. On this basis, this study also achieved the regulation of microstructure randomness and the generation of gradient materials through continuous interpolation in latent space using denoising diffusion implicit model (DDIM). Furthermore, the two-dimensional microstructure reconstruction was extended to three-dimensional framework and integrated permeability as a feature encoding embedding. This enables the conditional generation of three-dimensional microstructures for random porous materials within a defined permeability range. The permeabilities of these generated microstructures were further validated through the application of the lattice Boltzmann method. The above methods provide new ideas and references for material reverse design.
© 2024. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures
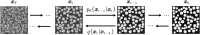





Similar articles
-
Freeze-Casting of Alumina and Permeability Analysis Based on a 3D Microstructure Reconstructed Using Generative Adversarial Networks.Materials (Basel). 2024 May 18;17(10):2432. doi: 10.3390/ma17102432. Materials (Basel). 2024. PMID: 38793499 Free PMC article.
-
Deep-learning-based porous media microstructure quantitative characterization and reconstruction method.Phys Rev E. 2022 Jan;105(1-2):015308. doi: 10.1103/PhysRevE.105.015308. Phys Rev E. 2022. PMID: 35193256
-
A Three-Dimensional Microstructure Reconstruction Framework for Permeable Pavement Analysis Based on 3D-IWGAN with Enhanced Gradient Penalty.Sensors (Basel). 2021 May 21;21(11):3603. doi: 10.3390/s21113603. Sensors (Basel). 2021. PMID: 34064274 Free PMC article.
-
Diffusion models in medical imaging: A comprehensive survey.Med Image Anal. 2023 Aug;88:102846. doi: 10.1016/j.media.2023.102846. Epub 2023 May 23. Med Image Anal. 2023. PMID: 37295311 Review.
-
An Overview of Deep Generative Models in Functional and Evolutionary Genomics.Annu Rev Biomed Data Sci. 2023 Aug 10;6:173-189. doi: 10.1146/annurev-biodatasci-020722-115651. Epub 2023 May 3. Annu Rev Biomed Data Sci. 2023. PMID: 37137168 Review.
Cited by
-
Deep learning for sub-ångström-resolution imaging in uncorrected scanning transmission electron microscopy.Natl Sci Rev. 2025 Jun 5;12(8):nwaf235. doi: 10.1093/nsr/nwaf235. eCollection 2025 Aug. Natl Sci Rev. 2025. PMID: 40755523 Free PMC article.
References
-
- Prifling B, Röding M, Townsend P, Neumann M, Schmidt V. Large-scale statistical learning for mass transport prediction in porous materials using 90,000 artificially generated microstructures. Front. Mater. 2021;8:786502.
-
- Wang Y, et al. Identifying interphase properties in polymer nanocomposites using adaptive optimization. Compos. Sci. Technol. 2018;162:146–155.
-
- Chen W, Iyer A, Bostanabad R. Data centric design: A new approach to design of microstructural material systems. Engineering. 2022;10:89–98.
-
- Bostanabad R, et al. Computational microstructure characterization and reconstruction: Review of the state-of-the-art techniques. Prog. Mater. Sci. 2018;95:1–41.
LinkOut - more resources
Full Text Sources
Miscellaneous

