Mathematical modelling of antibiotic interaction on evolution of antibiotic resistance: an analytical approach

Abstract

Background: The emergence and spread of antibiotic-resistant pathogens have led to the exploration of antibiotic combinations to enhance clinical effectiveness and counter resistance development. Synergistic and antagonistic interactions between antibiotics can intensify or diminish the combined therapy's impact. Moreover, these interactions can evolve as bacteria transition from wildtype to mutant (resistant) strains. Experimental studies have shown that the antagonistically interacting antibiotics against wildtype bacteria slow down the evolution of resistance. Interestingly, other studies have shown that antibiotics that interact antagonistically against mutants accelerate resistance. However, it is unclear if the beneficial effect of antagonism in the wildtype bacteria is more critical than the detrimental effect of antagonism in the mutants. This study aims to illuminate the importance of antibiotic interactions against wildtype bacteria and mutants on the deacceleration of antimicrobial resistance.

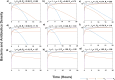
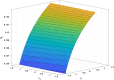
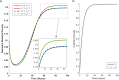
Methods: To address this, we developed and analyzed a mathematical model that explores the population dynamics of wildtype and mutant bacteria under the influence of interacting antibiotics. The model investigates the relationship between synergistic and antagonistic antibiotic interactions with respect to the growth rate of mutant bacteria acquiring resistance. Stability analysis was conducted for equilibrium points representing bacteria-free conditions, all-mutant scenarios, and coexistence of both types. Numerical simulations corroborated the analytical findings, illustrating the temporal dynamics of wildtype and mutant bacteria under different combination therapies.

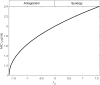
Results: Our analysis provides analytical clarification and numerical validation that antibiotic interactions against wildtype bacteria exert a more significant effect on reducing the rate of resistance development than interactions against mutants. Specifically, our findings highlight the crucial role of antagonistic antibiotic interactions against wildtype bacteria in slowing the growth rate of resistant mutants. In contrast, antagonistic interactions against mutants only marginally affect resistance evolution and may even accelerate it.

Conclusion: Our results emphasize the importance of considering the nature of antibiotic interactions against wildtype bacteria rather than mutants when aiming to slow down the acquisition of antibiotic resistance.

Keywords: Antibiotic; Antibiotic interaction; Differential equation; Equilibrium solutions.

Figure 1. Temporal course of sensitive (s) and resistant (r) bacteria population under three scenarios of antibiotics interaction for different values of R_s and R_r.

During the additive ( λ₁ = λ₂ = 0) effect of antibiotic interaction on both s and r bacteria for (A) infection-free (R_s < 1, R_r < 1), (D) all-resistance (R_s < 1, R_r > 1), and (G) coexistence (R_s > 1, R_r > 1) cases. During the synergistic ( λ₁ = 1) effect of antibiotic interaction on the s bacteria, and antagonistic ( λ₂ = −1) effect on r bacteria for (B) infection-free (R_s < 1, R_r < 1), (E) all-resistance (R_s < 1, R_r > 1), and (H) coexistence (R_s > 1, R_r > 1) cases. During the antagonistic ( λ₁ = −1) effect of antibiotic interaction on the s, and synergistic ( λ₂ = 1) effect on the r bacteria for (C) infection-free (R_s < 1, R_r < 1), (F) all-resistance (R_s < 1, R_r > 1), and (i) coexistence (R_s > 1, R_r > 1) cases. Here c₁ and c₂ are the concentration of antibiotics, M and N, respectively. Simulations are done using parameter values in Table 1 and bacteria and antibiotic concentration (y-axis) given in the log plot. The solution of system (5) approaches P₀ in (A–C), P₁ in (D–F), and P₂ in (G–I).

Figure 2. Minimum inhibitory concentration (MIC) of resistant bacteria as a result of antibiotic interaction.

Here, the y-axis displays the equivalent MIC while the x-axis displays the intensity of the interaction of antibiotics (λ₂) against resistant bacteria. The synergism and antagonism proxies are respectively when λ₂ > 0 and λ₂ < 0.

Figure 3. Correlation between antibiotic interaction level and growth rate of resistant strains.

The x-axis and y-axis in this graph show the level of antibiotic interaction with sensitive (λ1) and resistant (λ2) bacteria, respectively, while the z-axis shows the equivalent growth rate (Gr) of resistant strains. The synergism and antagonism proxies are respectively when λ1, λ2 > 0 and λ1, λ2 < 0.

Figure 4. Temporal course of resistant (r) bacteria population under different combination scenarios.

(A) Resistant bacteria population over time. (B) Antibiotic M (blue line) and N (red dash line) concentration (c₁) and (c₂), respectively, over time. In graph (A) blue line reveals the synergistic (λ₁ = 1) effect of M and N antibiotics on sensitive bacteria and the antagonistic (λ₂ = −1) effect of M and N antibiotics on resistant bacteria. The red line illustrates the antagonistic (λ₁ = −1) effect of M and N antibiotics on sensitive bacteria and the synergistic (λ₂ = 1) effect of M and N antibiotics on resistant bacteria. The black line shows the antagonistic (λ₁ = −1, λ₂ = −1) effect of M and N antibiotics on sensitive and resistant bacteria. The green line synergistic (λ₁ = 1, λ₂ = 1) effect of M and N antibiotics on sensitive and resistant bacteria. The rectangular dash point out the resistant bacteria population when the concentration of M and N antibiotics are at their maximum level (c₁ = c₂ = 1).