A maximum-likelihood method to estimate haplotype frequencies and prevalence alongside multiplicity of infection from SNP data

Abstract

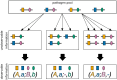
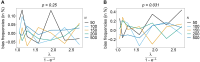
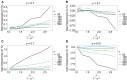
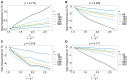
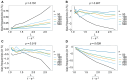
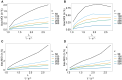
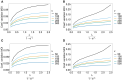
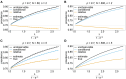
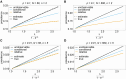
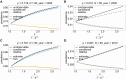
The introduction of genomic methods facilitated standardized molecular disease surveillance. For instance, SNP barcodes in Plasmodium vivax and Plasmodium falciparum malaria allows the characterization of haplotypes, their frequencies and prevalence to reveal temporal and spatial transmission patterns. A confounding factor is the presence of multiple genetically distinct pathogen variants within the same infection, known as multiplicity of infection (MOI). Disregarding ambiguous information, as usually done in ad-hoc approaches, leads to less confident and biased estimates. We introduce a statistical framework to obtain maximum-likelihood estimates (MLE) of haplotype frequencies and prevalence alongside MOI from malaria SNP data, i.e., multiple biallelic marker loci. The number of model parameters increases geometrically with the number of genetic markers considered and no closed-form solution exists for the MLE. Therefore, the MLE needs to be derived numerically. We use the Expectation-Maximization (EM) algorithm to derive the maximum-likelihood estimates, an efficient and easy-to-implement algorithm that yields a numerically stable solution. We also derive expressions for haplotype prevalence based on either all or just the unambiguous genetic information and compare both approaches. The latter corresponds to a biased ad-hoc estimate of prevalence. We assess the performance of our estimator by systematic numerical simulations assuming realistic sample sizes and various scenarios of transmission intensity. For reasonable sample sizes, and number of loci, the method has little bias. As an example, we apply the method to a dataset from Cameroon on sulfadoxine-pyrimethamine resistance in P. falciparum malaria. The method is not confined to malaria and can be applied to any infectious disease with similar transmission behavior. An easy-to-use implementation of the method as an R-script is provided.

Keywords: EM-algorithm; complexity of infection (COI); drug resistance; haplotype phasing; malaria; multiplicity of infection (MOI); resistance markers; sulfadoxine-pyrimethamine (SP).

Figure 1

Ambiguity in haplotype information for two biallelic loci. Illustrated are three different infections from the same pathogen population. The first infection (middle left) describes a super-infection with two haplotypes, i.e., MOI = 2. The corresponding observation (bottom left) provides only unphased (i.e., ambiguous) haplotype information. It is impossible to reconstruct with certainty the haplotypes actually present in the infection and the corresponding MOI. The second infection (middle), illustrates a super-infection with two haplotypes transmitted one and two times, respectively, i.e., MOI = 3. From the observed information, the haplotypes present in the infections can be unambiguously phased. However, MOI remains unknown. The last infection (middle right) is similar to the second, however with MOI = 4.

Figure 2

Bias of frequencies estimates—the symmetric case. Shown is the bias of the frequency estimates in % as a function of the mean MOI (i.e., for a range of Poisson parameters). The symmetric haplotype frequency distributions (cf. Table 1) for n = 2 (A) and n = 5 (B) are assumed. In both panels, only the bias for the first haplotype is shown (in the symmetric case, all haplotypes are equivalent and bias looks similarly). Colors correspond to different sample sizes.

Figure 3

Bias of frequencies estimates—the unbalanced case. Shown is the bias of the frequency estimates in % as a function of the mean MOI (i.e., for a range of Poisson parameters). The skewed haplotype frequency distributions (cf. Table 1) for n = 2 (A,B) and n = 5 (C,D) are assumed. In both cases only the bias for the predominant haplotype and one underrepresented haplotype are shown (all underrepresented haplotypes are equivalent and bias looks similarly). Colors correspond to different sample sizes.

Figure 4

Bias of frequencies estimates—Kenya data 2005. Shown is the bias of the frequency estimates in % as a function of the mean MOI (i.e., for a range of Poisson parameters). The haplotype frequency distributions (cf. Table 2) for n = 10 are assumed. The bias for the predominant haplotype and few underrepresented haplotype are shown (A–D), the corresponding haplotype frequencies are shown at the top of the panels. Colors correspond to different sample sizes.

Figure 5

Bias of frequencies estimates—Kenya data 2010. Shown is the bias of the frequency estimates in % as a function of the mean MOI (i.e., for a range of Poisson parameters). The haplotype frequency distributions (cf. Table 2) for n = 10 are assumed. The bias for the predominant haplotype and few underrepresented haplotype are shown (A–D), the corresponding haplotype frequencies are shown at the top of the panels. Colors correspond to different sample sizes.

Figure 6

Bias of MOI estimates. Shown is the bias of the mean MOI estimates ψ in % as a function of the true mean MOI (i.e., for a range of Poisson parameters). Symmetric haplotype frequency distributions (Table 1) are assumed for n = 2 (A) and n = 5 (B), whereas skewed distributions are assumed in (C,D), for n = 2 and n = 5, respectively. Colors correspond to different sample sizes.

Figure 7

Bias of MOI estimates. As in Figure 6 but for n = 10 for the haplotype estimated for antimalarial drug resistance in Kenya (see Table 2) in 2005 (A) and 2010 (B).

Figure 8

Variance of MOI estimates. Shown is the variance of the mean MOI estimates ψ in % as a function of the true mean MOI (i.e., for a range of Poisson parameters). The symmetric haplotype frequency distribution is assumed respectively for n = 2 and n = 5 (A,B) as well as the skewed haplotype frequency distributions (C,D) (cf. Table 1). Colors correspond to different sample sizes.

Figure 9

Variance of MOI estimates. Shown is the variance of the mean MOI estimates ψ in % as a function of the true mean MOI (i.e., for a range of Poisson parameters). The haplotype frequency distributions for n = 10 are assumed, respectively, for the year 2005 (A) and 2010 (B) (cf. Table 2). Colors correspond to different sample sizes.

Figure 10

Prevalence estimates—the symmetric case. Shown is the prevalence of the haplotypes as a function of the mean MOI (i.e., for a range of Poisson parameters). The symmetric haplotype frequency distributions (cf. Table 1) for n = 2 (A,B) and n = 5 (C,D) are assumed. In both cases of n only the prevalence estimates for the first haplotype are shown for a small (N = 50) and big (N = 500) sample size (in the symmetric case all haplotypes are equivalent and prevalence looks similarly). Colors correspond to different prevalence models. The solid line show the true prevalence and the dashed line the estimates.

Figure 11

Prevalence estimates—the unbalanced case. Shown is the prevalence of the predominant haplotypes as a function of the mean MOI (i.e., for a range of Poisson parameters). The skewed haplotype frequency distributions (cf. Table 1) for n = 2 (A,B) and n = 5 (C,D) are assumed. In both cases of n only the prevalence estimates are shown for a small (N = 50) and big (N = 500) sample size. Colors correspond to different prevalence models. The solid lines show the true prevalence and the dashed lines the estimates.

Figure 12

Prevalence estimates—the unbalanced case: Shown is the prevalence of the underrepresented haplotypes as a function of the mean MOI (i.e., for a range of Poisson parameters). The skewed haplotype frequency distributions (cf. Table 1) for n = 2 (A,B) and n = 5 (C,D) are assumed. In both cases of n only the prevalence of one of the underrepresented haplotypes estimates are shown for a small (N = 50) and big (N = 500) sample size (all underrepresented haplotypes are equivalent and prevalence looks similarly). Colors correspond to different prevalence models. The solid lines show the true prevalence and the dashed lines the estimates.

Figure 13

Prevalence estimates—the unbalanced case: Shown is the prevalence of the dominant and one underrepresented haplotype for the years 2005 (A,B) and 2010 (C,D) as a function of the mean MOI (i.e., for a range of Poisson parameters). The haplotype frequency distributions (cf. Table 2) for n = 10 are assumed. The prevalence estimates are shown for N = 50. Colors correspond to different prevalence models. The solid lines show the true prevalence and the dashed lines the estimates.