MVComp toolbox: MultiVariate Comparisons of brain MRI features accounting for common information across metrics

Abstract

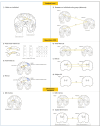
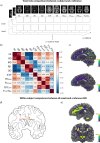
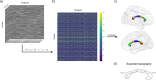
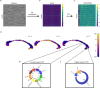
Multivariate approaches have recently gained in popularity to address the physiological unspecificity of neuroimaging metrics and to better characterize the complexity of biological processes underlying behavior. However, commonly used approaches are biased by the intrinsic associations between variables, or they are computationally expensive and may be more complicated to implement than standard univariate approaches. Here, we propose using the Mahalanobis distance (D2), an individual-level measure of deviation relative to a reference distribution that accounts for covariance between metrics. To facilitate its use, we introduce an open-source python-based tool for computing D2 relative to a reference group or within a single individual: the MultiVariate Comparison (MVComp) toolbox. The toolbox allows different levels of analysis (i.e., group- or subject-level), resolutions (e.g., voxel-wise, ROI-wise) and dimensions considered (e.g., combining MRI metrics or WM tracts). Several example cases are presented to showcase the wide range of possible applications of MVComp and to demonstrate the functionality of the toolbox. The D2 framework was applied to the assessment of white matter (WM) microstructure at 1) the group-level, where D2 can be computed between a subject and a reference group to yield an individualized measure of deviation. We observed that clustering applied to D2 in the corpus callosum yields parcellations that highly resemble known topography based on neuroanatomy, suggesting that D2 provides an integrative index that meaningfully reflects the underlying microstructure. 2) At the subject level, D2 was computed between voxels to obtain a measure of (dis)similarity. The loadings of each MRI metric (i.e., its relative contribution to D2) were then extracted in voxels of interest to showcase a useful option of the MVComp toolbox. These relative contributions can provide important insights into the physiological underpinnings of differences observed. Integrative multivariate models are crucial to expand our understanding of the complex brain-behavior relationships and the multiple factors underlying disease development and progression. Our toolbox facilitates the implementation of a useful multivariate method, making it more widely accessible.

Keywords: Multivariate analysis; covariance; personalized assessment; python; toolbox; white matter.

Fig. 1.

Implementations of the D2 framework in neuroimaging studies. Analysis level: (1) Within an individual (left panel, in light blue): D2 can be computed between different voxels or brain regions (e.g., WM tracts) within a single subject. (2) Between an individual and a group (right panel, in light gray): D2 can be computed between a subject and a reference group (e.g., control group). Resolution of D2: (a) Voxel-voxel matrix D2: D2 can be computed between each voxel and all other voxels in a mask of analysis, resulting in a D2 matrix of size n voxels × n voxels (only applicable to analyses within an individual). (b) Voxel-wise D2: A D2 value can be computed at each voxel. (c) ROI D2: In this case, a D2 value is obtained for each WM tract, or other brain region (ROI) defined by the user. (d) Subject D2: A single D2 value can be obtained per subject, resulting in a measure of global brain deviation from the reference (only applicable to analyses between an individual and a group). Dimensions combined: (i) MRI metrics: when the dimensions combined through D2 are MRI metrics, the length of the vector of data is the number of metrics. (ii) Spatial dimensions: when WM tracts, or other parcellated brain regions, are combined through D2, the length of the vector of data is equal to the number of WM tracts (only applicable to analyses between an individual and a group; yields a single D2 value per subject).

Fig. 2.

D2 workflow. Voxel-wise comparisons between a subject and a reference. (a) The multivariate space is illustrated here. In this example, we have a vector of 10 dMRI metrics at each WM voxel for each subject. (b) The covariance matrix is computed from the reference feature matrix of shape n voxels in WM × n features. The plot shows the amount of correlation between features in the reference sample (i.e., the whole group). (c) Voxel-wise D2 maps in two example subjects, where bright yellow represents areas of greater deviation from the reference population. Distinct patterns can be seen in the two subjects. Note that the leave-one-subject-out approach was used so that the data of the subject under evaluation was not included in the group mean (i.e., reference) and covariance matrix prior to D2 calculation. Within-subject comparisons between all WM voxels and a reference ROI. (d) Schematic representation of the multivariate comparisons showing that D2 was computed between all WM voxels and a ROI of 24 voxels in the corticospinal tract (CST). (e) D2 map showing the multivariate distance between all WM voxels and the CST ROI (in pink). *Data used for these examples will be presented in section 2.7.

Fig. 3.

Voxel-wise comparisons between each subject and the reference. (a) Voxel-wise D2 is calculated between the reference (group average of the whole sample, except the subject under evaluation) and each subject’s data (feature (10) × voxel (2845) matrix), in voxels of the corpus callosum (CC). (b) This results in a D2 matrix of size subject (723 after exclusion of outliers) × voxel (2845) containing the multivariate distance between a subject’s data and the reference at each CC voxel. (c) Applying k-means clustering to the D2 matrix, voxels of the CC were partitioned into 9 clusters distributed along the anterior-posterior axis, in close accordance with known topography of the CC as seen in (d). (d) Schematic representation of CC topography based on literature (Aboitiz et al., 1992; Chao et al., 2009; Hofer & Frahm, 2006).

Fig. 4.

Within-subject voxel-voxel comparisons. D2 was computed between all voxel pairs from the (a) (features) × (voxels in the CC) matrix of a subject. (b) A voxel × voxel D2 matrix was generated. (c) PCA was then applied to the D2 matrix. The PCA matrix shows the first 10 principal components. (d) Voxels with the highest and lowest score on PC1 are shown. PC1 scores were scaled between −10 and 10 to facilitate visualization. (e) In the voxel with the lowest value on PC1, located in the midbody of the CC, all metrics had approximately equal contribution to D2. (f) SumFDC contributed most to D2 in the voxel with the highest PC1 score, located in the genu of the CC.