Design, optimization, and inference of biphasic decay of infectious virus particles

Abstract

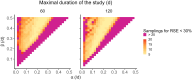
Virus population dynamics are driven by counter-balancing forces of production and loss. Whereas viral production arises from complex interactions with susceptible hosts, the loss of infectious virus particles is often approximated as a first-order kinetic process. As such, experimental protocols to measure infectious virus loss are not typically designed to identify non-exponential decay processes. Here, we propose methods to evaluate if an experimental design is adequate to identify multiphasic virus particle decay and to optimize the sampling times of decay experiments, accounting for uncertainties in viral kinetics. First, we evaluate synthetic scenarios of biphasic decays, with varying decay rates and initial proportions of subpopulations. We show that robust inference of multiphasic decay is more likely when the faster decaying subpopulation predominates insofar as early samples are taken to resolve the faster decay rate. Moreover, design optimization involving non-equal spacing between observations increases the precision of estimation while reducing the number of samples. We then apply these methods to infer multiple decay rates associated with the decay of bacteriophage ('phage') $\Phi \text{D}9$ , an evolved isolate derived from phage $\Phi 21$ . A pilot experiment confirmed that $\Phi \text{D}9$ decay is multiphasic, but was unable to resolve the rate or proportion of the fast decaying subpopulation(s). We then applied a Fisher information matrix-based design optimization method to propose non-equally spaced sampling times. Using this strategy, we were able to robustly estimate multiple decay rates and the size of the respective subpopulations. Notably, we conclude that the vast majority (94%) of the phage $\Phi \text{D}9$ population decays at a rate 16-fold higher than the slow decaying population. Altogether, these results provide both a rationale and a practical approach to quantitatively estimate heterogeneity in viral decay.

Keywords: Fisher information matrix; inference; multiphasic decay; optimal design; viral decay.

Figure 1:. Influence of the viral parameters on a biphasic decay.

Biphasic decays (eq. 6) are represented on the two panels: with different decay rates for one population $\left(\beta \right)$ ranging from 0.05 to 1 /d (with same initial proportions for both populations i.e., $f_a=f_b=0.5$ and decay rate of the other population $\left(\alpha \right)$ of 0.35 /d) on the left and different initial proportions $f_a$ ranging from 0.05 to 0.95 (with $f_b=1-f_a,\alpha =0.1/\text{d}$ and $\beta =0.3/\text{d}$) on the right.

Figure 2:. Influence of viral parameters on maximal imprecision (RSE) of estimates using an (A) empirical non-optimized design or an (B) optimized design and on (C) optimal sampling times.

The non-optimized design consists in 7 measuring times from 0 to 60 days every 10 days. The design optimization is performed by the simplex algorithm (7 times in the [0–60] days window), where $\alpha$ is the decay rate of the slowest virus, $\beta$ is the decay rate of the fastest virus, $f_a$ and $f_b=1-f_a$ are the initial proportions (corresponding to $\alpha$ and $\beta$, respectively). RSE refers to relative standard error and the color represents the higher expected RSE among the estimated parameters: $\alpha ,\beta ,f_a,f_b$ and $\sigma$ (the error model parameter). Optimal designs are represented for different parameters combinations by specific symbols $(\alpha =0.06/\text{d}$, square: $\beta =0.46/\text{d}$ and $f_a=0.25$, rotated square: $\beta =0.16/\text{d}$ and $f_a=0.25$, triangle: $\beta =0.46/\text{d}$ and $f_a=0.75$, circle: $\beta =0.16/\text{d}$ and $\left.f_a=0.75\right)$.

Figure 3:. Influence of maximal duration time on needed sampling times to reach adequate precision of estimation.

A flexible number of measuring times is considered between 0 and 60 days on the left and between 0 and 120 days on the right, respectively. Sampling times of the design are optimized using the simplex algorithm in the corresponding sampling window ([0,60] and [0,120]). $\alpha$ is the decay rate of the slowest virus, $\beta$ is the decay rate of the fastest virus, the initial proportion of each viral population is 0.5. RSE: Relative Standard Error.

Figure 4:. Design comparison for expected coverage of parameter precision.

Coverage is the percentage of parameter settings ($\alpha$ from 0.02 to 0.48 /d (increment of 0.02), $\beta (>\alpha )$ from 0.04 to 0.5 /d, $f_a$ and $f_b$ among (0.05, 0.25, 0.5, 0.75 or 0.95, with $f_a+f_b=1$) that the different design strategies allow to reach an expected RSE (Relative Standard Error) of 30% (left) or 50% (right) for the different parameters.

Figure 5:. Phage ΦD9 decay data fitting from (A) the non-optimized pilot experiment and (B) the optimized design.

Red line is the viral density decay prediction from the biexponential model (eq. 6) and the parameters given in Table 2. The pilot experiment was composed of two batches with theoretical sampling times at 0, 1, 2, 4, 5, and 7 days for one batch and 0, 1, 2, 4, and 7 days for the other batch. Six replicates were made for each measurement of the pilot experiment. The optimized design experiment was composed of one batch with theoretical sampling times at 0, 0.04, 0.08, 0.13, 0.21, 0.33, 1, 2, and 3 days (i.e., 0, 1, 2, 3, 5, 8, 24, 48, and 72 hours). Twelve replicates were made for each measurement of the optimized experiment.