The recovery of parabolic avalanches in spatially subsampled neuronal networks at criticality

Abstract

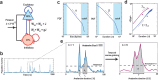
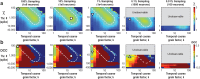
Scaling relationships are key in characterizing complex systems at criticality. In the brain, they are evident in neuronal avalanches-scale-invariant cascades of neuronal activity quantified by power laws. Avalanches manifest at the cellular level as cascades of neuronal groups that fire action potentials simultaneously. Such spatiotemporal synchronization is vital to theories on brain function yet avalanche synchronization is often underestimated when only a fraction of neurons is observed. Here, we investigate biases from fractional sampling within a balanced network of excitatory and inhibitory neurons with all-to-all connectivity and critical branching process dynamics. We focus on how mean avalanche size scales with avalanche duration. For parabolic avalanches, this scaling is quadratic, quantified by the scaling exponent, $\chi =\text{2}$ , reflecting rapid spatial expansion of simultaneous neuronal firing over short durations. However, in networks sampled fractionally, $\chi$ is significantly lower. We demonstrate that applying temporal coarse-graining and increasing a minimum threshold for coincident firing restores $\chi =\text{2}$ , even when as few as 0.1% of neurons are sampled. This correction crucially depends on the network being critical and fails for near sub- and supercritical branching dynamics. Using cellular 2-photon imaging, our approach robustly identifies $\chi =\text{2}$ over a wide parameter regime in ongoing neuronal activity from frontal cortex of awake mice. In contrast, the common 'crackling noise' approach fails to determine $\chi$ under similar sampling conditions at criticality. Our findings overcome scaling bias from fractional sampling and demonstrate rapid, spatiotemporal synchronization of neuronal assemblies consistent with scale-invariant, parabolic avalanches at criticality.

Keywords: 2-photon imaging; E/I balanced neural network; Neuronal avalanches; criticality; frontal cortex; mouse; ongoing activity; scaling exponent; subsampling; thresholding.

Figure 1.. Schematics of the balanced E/I-model and identification of suprathreshold sequences in population spiking activity with respect to minimal coincident spiking threshold and temporal coarse graining.

(a) Schematic of the neuronal network consisting of N = 10⁶ neurons (80% excitatory and 20% inhibitory) with a low external Poisson drive of rate λ = 2*10–5 per time step per neuron. The E/I balance is controlled by $g$, which scales the inhibitory weight matrices (${\text{W}}_{\text{II}}$, ${\text{W}}_{\text{EI}}$) as a function of the excitatory weight matrices (${\text{W}}_{\text{EE}}$, ${\text{W}}_{\text{IE}}$). If not otherwise stated, we set $g=3.5$ to obtain critical dynamics (see Methods). (b) High variability in intermittent population activity characterizes critical dynamics. Snapshot of the summed neuronal spiking activity as a function of time. (c) Size and duration of avalanches in the critical model follow power-laws with corresponding exponent estimates $\alpha$ and $\beta$, respectively. Note that the external Poisson drive and the finite size of the network introduce lower and higher cut-offs, respectively (shaded areas). (d) Scaling of mean avalanche size as a function of duration also follows a power-law. $\chi$ is the estimate of the scaling exponent for short avalanches (below cut-off point, ▲). Avalanches within the upper cut-off (above cut-off point, ▲) exhibit a trivial scaling exponent close to 1, denoted as ${\chi }_{lg}$, that is largely independent of threshold and temporal coarse-graining and will not be considered further. Purple: Corresponding scaling relation and cut-off for temporal coarse-graining with k = 5 (see below). (e) Zoomed population activity from $B$. At the original temporal resolution $\Delta t$ and given the coincident spiking threshold, $\theta$(left), we can identify two sequences of suprathreshold activity, $S_1$ and $S_2$ with durations $T_1$ and $T_2$, respectively. Temporally coarse-graining the population activity (right;$k=5$, binning the data into new bins of 5 time points) and increasing the threshold to θ’ > θ, absorbs $S_1$ and $S_2$ into a new suprathreshold activity period T’ with size S’ with corresponding change in scaling (see also d).

Figure 2.. Increasing the threshold in the fully sampled model underestimates the scaling exponent, χ, which can be rescued by temporal coarse graining.

(a) Consolidated view of the avalanche size ($\alpha$), duration ($\beta$), and scaling ($\chi$) exponents as a function of threshold $\theta$ and temporal coarse-graining factor $k$ (f = 100%, fully sampled model). Drive dominated: Low threshold regime (above the red broken line) dominated by external Poisson drive. White frames: Parameter regions displayed in b and c. (b) At the highest temporal resolution ($k=1$), high thresholds underestimate the scaling exponent, $\chi$, as well as ${\chi }_{cn}$, with DCC remaining low. Size exponent, $\text{α}$(left), duration exponent, $\text{β}$(middle), scaling exponent, $\chi$, and expected crackling noise relation, ${\chi }_{cn}$, (right) as a function of $\theta$. (c) At highthreshold (θ =1000), temporal coarse graining recovers $\chi$, but the ${\chi }_{cn}$ exhibits a singularity leading to high DCC. Size exponent, $\text{α}$(left), duration exponent, $\text{β}$(middle), as a function of coarse graining factor, $\text{k}$, ($\theta =1000$). $\text{α}$ passes through 1 (red broken line; black triangle), which causes a singularity in ${\chi }_{cn}$_. (right). Note that the scaling exponent, $\chi$, stabilizes to a value of 2 (right, black dashed line), whereas ${\chi }_{cn}$ grows until it passes through a singularity at the temporal coarse graining value of $k=17$ (vertical broken line; triangle; see inset).

Figure 3.. Temporal coarse graining at critical value of g: Rescue of scaling exponent, equivalence between threshold and fractional sampling, and increased mean pairwise neuron correlation.

(a) The maximum scaling exponent across different temporal binning values as a function of the balance parameter, $g$, for a subsampled model (f = 0.1%) employing a 1-spike threshold. Notably, the retrieval of $\text{χ}=2$ is exclusively observed in critical models ($g_c=3.5$), but promptly diminishes in slightly subcritical or supercritical models. In supercritical models, we obtain ceaseless activity (shaded gray region), precluding the identification of avalanches at the specified threshold. Yellow circles mark g values used in c. (b) Collapsed scaling exponent curves for different values of the sampling fraction, $f$, ranging from 100% to 0.1% for a threshold that is scaled by the sampling fraction as θ = 3,000*f (i.e., a threshold of 3,000 spikes for the fully sampled model translates to a threshold of 3 spikes for the 0.1% sampled model). Inset: The total collapse error as a function of collapse exponent, $\xi$. The error is taken over multiple different curves with $\theta$ ranging from 100 to 100,000. The error shows a clear minimum at $\xi =1$, indicating the threshold can be scaled proportionally with the sampling fraction to obtain the best collapse. (c) The rescue of $\chi =2$ correlates with an increase of the mean delayed pair-wise correlation among neurons, which is independent of the fraction of neurons sampled. However, the temporal coarse graining regime of k for which $\chi =2$ (green area) is not predicted by this pair-wise correlation. For a supercritical ($g=3.475$) network, the mean pairwise correlation is lower, but still increases with temporal coarse graining. For a subcritical network ($g=3.6$), the mean delayed pair-wise correlation is close to 0.

Figure 4.. Temporal coarse -graining identifies a robust rescue regime for χ=2 covering 0.1% – 100% fractional sampling at decreasing thresholding level, which is absent for the DCC

(a) Consolidated view of $\chi$ as a function of θ and k for different values of $f$. For f = 100%, $\chi \widetilde{=}2$ for low $\theta$ and $k$ (star) but as we make the data sparser by increasing the threshold (or reducing the sampling), we need a higher coarse graining factor, $k$, to compensate and rescue $\chi$ back to 2 (square). White dotted region: visual guide for $\chi$ close to 2 for increasing $\theta$ and $k$. The grey parts of the plots for f = 0.1% and 0.01% respectively are unobservable parameter regions since they would require fractional thresholds, below the 1 spike minimum resolution of the model. At f = 0.1% sampling, $\chi$ can be rescued to a value of 2, but not for more severe subsampling, f = 0.01%. For triangles see b. (b) The DCC remains close to 0 only for low k, and quickly breaks down at higher $k$ values. For the fully sampled model, there exists a region with the correct scaling exponent $\chi \cong 2$ as well as low DCC (star in A and B) However, as we move to lower sampling, this region of correspondence becomes more and more difficult to maintain. For f = 1% and 0.1%, regions at low k, and moderate threshold (or equivalently lower sampling) remain at low DCC, but underestimate the true scaling exponent, $\chi$(up and down triangles, respectively).

Figure 5.. Parabolic avalanches in ongoing activity of frontal cortex exhibit threshold and temporal coarse-graining rescue of scaling exponent χ=2 in line with critical model dynamics.

(a) Lognormal distribution of avalanche number as a function of threshold for 17 different recordings ($n=5$ mice; 2-photon imaging of ongoing activity in frontal cortex) at the original temporal resolution ($\Delta =t$, black) and after temporal coarse graining ($k=10$, purple). Note the experimental variability at a given $k$, as well as the systematic shift in the distribution with change in $k$. A sample threshold ($\theta$, grey dotted) shows how a given fixed threshold relates to these distributions. (b) Scaling exponent, $\chi$, and (c) crackling noise deviation, DCC, as a function of temporal coarse grain factor, $k$ and the spike density thresholds. The subregion in which $\chi \widetilde{=}2$ (broken line) is similar to the one identified in the critically balanced E-I model. At low thresholds, the scaling is rescued at smaller values of temporal coarse graining factor, k and at high thresholds, it is rescued at a larger value of $k$. Over this large range of parameters, the DCC is very noisy even a small change in the parameters can cause a large change in the DCC. (d) Z-scoring procedure for the lognormal distributions corrects for experimental variability as well as temporal coarse graining. A sample z-scored threshold (${\theta }_{z,k}$, grey dotted) shows how a given z-scored threshold relates to these distributions. (e) Scaling exponent, $\chi$, and (f) crackling noise deviation, DCC, as a function of temporal coarse grain factor, $k$, and the z-scored threshold at the given $k$, ${\theta }_{z,k}$. Figure D shows a robust rescue of $\chi \widetilde{=}2$ (broken line) for a large range of z-scored threshold values (−1.5 to 1.5). The range of k values over which $\chi \widetilde{=}2$ becomes smaller with an increase in the z-scored threshold. Like B, Figure E shows that the DCC remains unreliable and noisy even when the thresholds are z-scored and tuned for each $k$.