A mathematical model to assess the effectiveness of test-trace-isolate-and-quarantine under limited capacities

Abstract

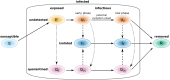
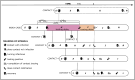
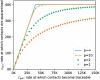
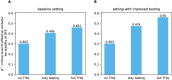
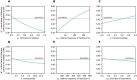
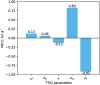
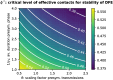
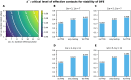
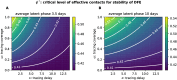
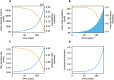
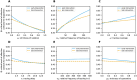
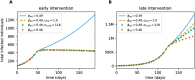
Diagnostic testing followed by isolation of identified cases with subsequent tracing and quarantine of close contacts-often referred to as test-trace-isolate-and-quarantine (TTIQ) strategy-is one of the cornerstone measures of infectious disease control. The COVID-19 pandemic has highlighted that an appropriate response to outbreaks of infectious diseases requires a firm understanding of the effectiveness of such containment strategies. To this end, mathematical models provide a promising tool. In this work, we present a delay differential equation model of TTIQ interventions for infectious disease control. Our model incorporates the assumption of limited TTIQ capacities, providing insights into the reduced effectiveness of testing and tracing in high prevalence scenarios. In addition, we account for potential transmission during the early phase of an infection, including presymptomatic transmission, which may be particularly adverse to a TTIQ based control. Our numerical experiments inspired by the early spread of COVID-19 in Germany demonstrate the effectiveness of TTIQ in a scenario where immunity within the population is low and pharmaceutical interventions are absent, which is representative of a typical situation during the (re-)emergence of infectious diseases for which therapeutic drugs or vaccines are not yet available. Stability and sensitivity analyses reveal both disease-dependent and disease-independent factors that impede or enhance the success of TTIQ. Studying the diminishing impact of TTIQ along simulations of an epidemic wave, we highlight consequences for intervention strategies.

Fig 1. Flowchart of the transmission model (1) with TTIQ interventions.

Solid lines indicate state transitions due to disease spread and disease progression. Dashed lines indicate confirmation and isolation of infectious cases due to testing. Dotted lines indicate quarantine of infected contacts due to contact tracing.

Fig 2. Possible timeline of events for an index case detected by testing at time t − κ and contacts made during the tracing interval J_T(t) for which the index case is asked to disclose close contacts from.

In the example shown above the tracing interval J_T(t) is longer than the testing delay, which results in Contact 1 being reported although Contact 1 could not have been infected by the index case. Contact 2 gets infected early during the infectious phase $J_T^{\text{inf}}\left(t\right)$ of the tracing interval. The time lag resulting from the testing and tracing delay leads to confirmation of Contact 2 by testing before time t of close contact notification. Contact 3 is an example of an individual that got infected but is missed by the tracing process. This might happen because the contact is not covered by the close contact definition or cannot be recalled by the index case. Contact 4 and 6 get infected late in $J_T^{\text{inf}}\left(t\right)$ shortly before the index case is confirmed as infectious by testing. Therefore, these contacts are less affected by the testing delay, leading to Contact 4 being undetected but infectious and Contact 6 still being latent by the time of being traced t. Contact 5 is categorized as a close contact of the index case and is therefore traced even though no transmission took place. When calculating the tracing efficiency, we account for the tracing effort contacts like 1 and 5 generate, however we do not consider the effect of their quarantine on the outbreak dynamics.

Fig 3. Illustration of Eq (6) for the choice Ω = 40 000 and multiple values of p.

The limit p → ∞ recovers Eq (5). Mind the different scaling of the axes.

Fig 4. Critical level ϕ* of effective contacts for the stability of the DFE.

Here we compare a scenario without any TTIQ (no TTIQ), a scenario where only testing is conducted (only testing) and a scenario where testing and tracing is carried out (full TTIQ). This is shown for A the baseline parameter setting given in Table 2 and B a setting with improved testing such that ${\sigma }_{U_2}=185$.

Fig 5. Critical level ϕ* of effective contacts for the stability of the DFE (solid lines) varying single TTIQ parameters.

For comparison we also indicate the value of ϕ* derived from our baseline parameter setting given in Table 2 (dashed line).

Fig 6. Critical level ϕ* of effective contacts for the stability of the DFE varying TTIQ parameters simultaneously.

This is shown for A the strictness of quarantine ρ_Q and the relative frequency ${\sigma }_{Q_U}$ of testing traced contacts, B the relative frequency ${\sigma }_{U_2}$ of testing undetected late infectious individuals assuming either strict quarantine and isolation (ρ_Q, ρ_I) = (0.2, 0.1) (solid line) or weak quarantine and isolation (ρ_Q, ρ_I) = (0.7, 0.35) (dashed line) and C the relative frequency ${\sigma }_{U_2}$ of testing undetected late infectious individuals and the tracing coverage ω.

Fig 7. Global sensitivity of the critical level ϕ* of effective contacts for the stability of the DFE with respect to TTIQ parameters.

The PRCC values where obtained using latin hypercube sampling on the parameter space specified in Table 3.

Fig 8. Critical level ϕ* of effective contacts for the stability of the DFE varying disease characteristics.

Here we vary the average duration of the early infectious period 1/γ₁ and the scaling factor θ for the early infectious transmission rate.

Fig 9. Critical level ϕ* of effective contacts for the stability of the DFE varying disease characteristics.

Here we vary the average duration of the latent phase 1/α and the average duration of the infectious period 1/γ. This is shown for A the (1/γ, 1/α)-plane and B-E different combinations of values for 1/α and 1/γ, comparing a scenario without any TTIQ to a scenario where only testing is conducted and a scenario where both testing and contact tracing is carried out.

Fig 10. Critical level ϕ* of effective contacts for the stability of the DFE varying the tracing delay κ and the tracing coverage ω.

This is shown assuming an average latent phase of either A 3.5 days or B 10 days.

Fig 11. Model outcomes simulating an outbreak starting from low case numbers.

This simulation is initiated using the baseline parameter values given in Table 2 and a reduction of effective contacts corresponding to ϕ = 0.6.

Fig 12. Critical level ϕ¯ of effective contacts that yields a stagnation in the incidence of infected individuals.

$\overline{\varphi }$ is calculated along the epidemic outbreak considered in Fig 11 and plotted against the timing of intervention t*. This is shown for different values of A the tracing capacity Ω, B the tracing efficiency constant p, C the testing capacity σ₊ and D comparing a scenario with high tracing capacity Ω and low tracing efficiency constant p to a scenario with low Ω and large p.

Fig 13. Critical level ϕ¯ of effective contacts that yields a stagnation in the incidence of infected individuals varying single TTIQ parameters.

This is shown for an early intervention time point corresponding to a daily case incidence of approximately 1 500 (solid lines) and for a late intervention time point corresponding to a daily case incidence of approximately 20 000 (dashed lines).

Fig 14. Number of infected individuals (both detected and undetected) simulating the baseline outbreak scenario from Fig 11 with different interventions.

Here an intervention takes place either A early at a daily case incidence of approximately 1 500 (t* = 47) or B late at a daily case incidence of approximately 20 000 (t* = 123). At the time of intervention the level of effective contacts is changed from its baseline value to ϕ_int. Additionally, in some considered scenarios, the tracing coverage is improved to ω_int or the relative frequency of testing undetected infectious individuals to ${{\sigma }_{U_2}}_{\text{int}}$. Parameters not mentioned in the legend are held constant throughout the simulation.