4D microvelocimetry reveals multiphase flow field perturbations in porous media
- PMID: 38478686
- PMCID: PMC10962996
- DOI: 10.1073/pnas.2316723121
4D microvelocimetry reveals multiphase flow field perturbations in porous media
Abstract
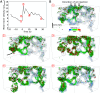
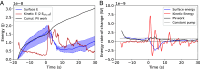
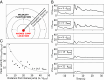
Many environmental and industrial processes depend on how fluids displace each other in porous materials. However, the flow dynamics that govern this process are still poorly understood, hampered by the lack of methods to measure flows in optically opaque, microscopic geometries. We introduce a 4D microvelocimetry method based on high-resolution X-ray computed tomography with fast imaging rates (up to 4 Hz). We use this to measure flow fields during unsteady-state drainage, injecting a viscous fluid into rock and filter samples. This provides experimental insight into the nonequilibrium energy dynamics of this process. We show that fluid displacements convert surface energy into kinetic energy. The latter corresponds to velocity perturbations in the pore-scale flow field behind the invading fluid front, reaching local velocities more than 40 times faster than the constant pump rate. The characteristic length scale of these perturbations exceeds the characteristic pore size by more than an order of magnitude. These flow field observations suggest that nonlocal dynamic effects may be long-ranged even at low capillary numbers, impacting the local viscous-capillary force balance and the representative elementary volume. Furthermore, the velocity perturbations can enhance unsaturated dispersive mixing and colloid transport and yet, are not accounted for in current models. Overall, this work shows that 4D X-ray velocimetry opens the way to solve long-standing fundamental questions regarding flow and transport in porous materials, underlying models of, e.g., groundwater pollution remediation and subsurface storage of CO2 and hydrogen.
Keywords: 3D velocimetry; hydrogeology; multiphase flow; porous media.
Conflict of interest statement
Competing interests statement:The authors declare no competing interest.
Figures

Similar articles
-
Multiscale drainage dynamics with Haines jumps monitored by stroboscopic 4D X-ray microscopy.Proc Natl Acad Sci U S A. 2024 Jan 2;121(1):e2305890120. doi: 10.1073/pnas.2305890120. Epub 2023 Dec 26. Proc Natl Acad Sci U S A. 2024. PMID: 38147554 Free PMC article.
-
Optimizing pink-beam fast X-ray microtomography for multiphase flow in 3D porous media.J Microsc. 2020 Feb;277(2):100-106. doi: 10.1111/jmi.12872. Epub 2020 Feb 13. J Microsc. 2020. PMID: 32022271
-
A review of non-invasive imaging methods and applications in contaminant hydrogeology research.J Contam Hydrol. 2010 Apr 1;113(1-4):1-24. doi: 10.1016/j.jconhyd.2010.01.001. Epub 2010 Jan 28. J Contam Hydrol. 2010. PMID: 20163885 Free PMC article. Review.
-
Capillary flows across layers and textural interfaces - Pathways and colloid transport considerations in unsaturated layered porous media.J Colloid Interface Sci. 2017 Oct 15;504:294-304. doi: 10.1016/j.jcis.2017.05.019. Epub 2017 May 10. J Colloid Interface Sci. 2017. PMID: 28551524
-
High pressure-elevated temperature x-ray micro-computed tomography for subsurface applications.Adv Colloid Interface Sci. 2018 Jun;256:393-410. doi: 10.1016/j.cis.2017.12.009. Epub 2017 Dec 28. Adv Colloid Interface Sci. 2018. PMID: 29526246 Review.
References
-
- Blunt M. J., Multiphase Flow in Permeable Media: A Pore-Scale Perspective (Cambridge University Press, 2017).
-
- Armstrong R. T., et al. , Beyond Darcy’s law: The role of phase topology and ganglion dynamics for two-fluid flow. Phys. Rev. E 94, 043113 (2016). - PubMed
-
- Bottero S., Hassanizadeh S. M., Kleingeld P. J., Heimovaara T. J., Nonequilibrium capillarity effects in two-phase flow through porous media at different scales. Water Resour. Res. 47, W10505 (2011).
-
- Rodríguez de Castro A., Shokri N., Karadimitriou N., Oostrom M., Joekar-Niasar V., Experimental study on nonmonotonicity of Capillary Desaturation Curves in a 2-D pore network. Water Resour. Res. 51, 8517–8528 (2015).
Grants and funding
LinkOut - more resources
Full Text Sources

