Perfect Matchings with Crossings

Abstract

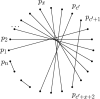
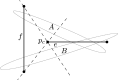
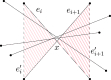
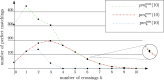
For sets of n points, n even, in general position in the plane, we consider straight-line drawings of perfect matchings on them. It is well known that such sets admit at least $C_{n/2}$ different plane perfect matchings, where $C_{n/2}$ is the n/2-th Catalan number. Generalizing this result we are interested in the number of drawings of perfect matchings which have k crossings. We show the following results. (1) For every $k\le \frac{1}{64}{n}^2-\frac{35}{32}n\sqrt{n}+\frac{1225}{64}n$, any set with n points, n sufficiently large, admits a perfect matching with exactly k crossings. (2) There exist sets of n points where every perfect matching has at most $\frac{5}{72}{n}^2-\frac{n}{4}$ crossings. (3) The number of perfect matchings with at most k crossings is superexponential in n if k is superlinear in n. (4) Point sets in convex position minimize the number of perfect matchings with at most k crossings for $k=0,1,2$, and maximize the number of perfect matchings with $\left(\begin{array}{c}n/2\\ 2\end{array}\right)$ crossings and with $\left(\begin{array}{c}n/2\\ 2\end{array}\right)-1$ crossings.

Keywords: Combinatorial geometry; Crossings; Geometric graphs; Order types; Perfect matchings.

Fig. 1

Illustration for the proof of Theorem 2: A point set P for which every perfect matching has $\le \frac{5n^2}{72}-\frac{n}{4}$ crossings (left). Interior ($I_1$) and outgoing ($O_0,O_1$) matching edges for wing 1 of P (right)

Fig. 2

Proof of Lemma 3: Matching with 42 crossings obtained from a crossing family of size $c^{\prime }=9$ plus $x=6$ extra crossings

Fig. 3

A set of 30 points with a perfect matching with $\left(\begin{array}{c}15\\ 2\end{array}\right)=105$ crossings, but with no perfect matching with $k\in \{103,104\}$ crossings. This result is obtained by direct computation

Fig. 4

The case where the non-crossing edges e and f are in non-convex position

Fig. 5

The pink shaded area represents the butterfly region of $e_i$ and $e_{i+1}$. If the butterfly region is empty of points, then any edge that crosses $e_i$ and $e_{i+1}$ also crosses $e_i^{\prime }$ and $e_{i+1}^{\prime }$

Fig. 6

Comparison of ${\text{pm}}_k^{min}(n)$, ${\text{pm}}_k^{max}(n)$, and ${\text{pm}}_k^{\text{conv}}(n)$ for $n=10$ and $0\le k\le 10$

Fig. 7

An illustration of the proof of Theorem 8 for $k=2$ crossings

Fig. 8

For $k=3$ crossings, the proof of Theorem 8 does not work: For the convex set (left) the given matching has three crossings. When drawing the edges on the second set (right) in the order given by the proof as indicated, an additional crossing occurs