Optimizing competence in the service of collaboration

Abstract

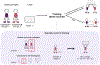
In order to efficiently divide labor with others, it is important to understand what our collaborators can do (i.e., their competence). However, competence is not static-people get better at particular jobs the more often they perform them. This plasticity of competence creates a challenge for collaboration: For example, is it better to assign tasks to whoever is most competent now, or to the person who can be trained most efficiently "on-the-job"? We conducted four experiments (N=396) that examine how people make decisions about whom to train (Experiments 1 and 3) and whom to recruit (Experiments 2 and 4) to a collaborative task, based on the simulated collaborators' starting expertise, the training opportunities available, and the goal of the task. We found that participants' decisions were best captured by a planning model that attempts to maximize the returns from collaboration while minimizing the costs of hiring and training individual collaborators. This planning model outperformed alternative models that based these decisions on the agents' current competence, or on how much agents stood to improve in a single training step, without considering whether this training would enable agents to succeed at the task in the long run. Our findings suggest that people do not recruit and train collaborators based solely on their current competence, nor solely on the opportunities for their collaborators to improve. Instead, people use an intuitive theory of competence to balance the costs of hiring and training others against the benefits to the collaboration.

Keywords: Collaboration; Competence; Planning; Plasticity; Social cognition; Teaching; Training.

Figure 1:

Example contest in Experiment 1. Participants saw two agents of varying strengths and a target box. They had three rounds to train the agents. In each round of training, they could either assign a box to an agent or not train anyone. Agents gained strength equivalent to the level of effort they put forth. After training, agents attempted to lift the target box together.

Figure 2:

Experiment 1 results. (A) Data and model predictions of agents’ strength in each round of training. Each subplot corresponds to one scenario, where the x-axis shows the weaker agent’s strength, the y-axis shows the stronger agent’s strength, and each line traces agents’ average strength in each training trial. The dashed black line marks the threshold where agents’ combined strength exceeds the target box weight; intuitively, if participants are balancing the costs and benefits of training, they should train agents until their combined strength reaches this threshold, and no further. Error bars indicate 95% confidence intervals. (B) Individual participants’ training trajectories. Each subplot denotes a scenario, and each arrow denotes a particular training strategy; the color of the arrow indicates how many participants adopted this strategy. For simplicity, here we represent each training strategy by showing only agents’ strength before (origin) and after training (arrowhead). The dashed black line marks the threshold where agents’ combined strength exceeds the target box weight.

Figure 3:

Distribution of model evidences for each participant (approximated as −0.5BIC) in (A) Experiment 1, (B) Experiment 2, (C) Experiment 3, and (D) Experiment 4.

Figure 4:

The four candidates in Experiment 2. Hiring costs are proportional to agents’ strength.

Figure 5:

Experiment 2 results. (A) Data and model predictions, showing the probability of choosing each team. Each subplot corresponds to one scenario; the brackets on the x-axis labels refer to the strength combinations of the two hired agents. Error bars indicate 95% confidence intervals of proportions. (B) Individual participants’ training trajectories of the modal teams. Each subplot denotes a scenario, and each arrow denotes a particular training strategy; the color of the arrow indicates how many participants adopted this strategy. For simplicity, here we represent each training strategy by showing only agents’ strength before (origin) and after training (arrowhead). The dashed black line marks the threshold where agents’ combined strength exceeds the target box weight.

Figure 6:

Experiment 3 data and model predictions of agents’ math level in every round of training. Each subplot corresponds to one scenario, where the x-axis shows the math level of the agent who was worse at math, the y-axis shows the math level of the agent who was better at math, and each line traces agents’ average math level in each training trial. The dashed black line marks the threshold where agents’ combined math level exceeds the target difficulty level of the contest; intuitively, if participants are balancing the costs and benefits of training, they should train agents until their combined math level reaches this threshold, and no further. Error bars indicate 95% confidence intervals.

Figure 7:

Experiment 3 individual participants’ training trajectories. Each subplot denotes a scenario, and each arrow denotes a particular training strategy; the color of the arrow indicates how many participants adopted this strategy. For simplicity, here we represent each training strategy by showing only agents’ math levels before (origin) and after training (arrowhead). The dashed black line marks the threshold where agents’ combined math level exceeds the target difficulty level of the contest.

Figure 8:

Experiment 4 results. (A) Data and model predictions, showing the probability of choosing each team. Each subplot corresponds to one scenario; the brackets on the x-axis labels refer to the math levels of the two recruited students. Error bars indicate 95% confidence intervals of proportions. (B) Individual participants’ training trajectories of the modal teams. Each subplot denotes a scenario, and each arrow denotes a particular training strategy; the color of the arrow indicates how many participants adopted this strategy. For simplicity, here we represent each training strategy by showing only agents’ math levels before (origin) and after training (arrowhead). The dashed black line marks the threshold where agents’ combined math level exceeds the target difficulty level of the contest.