Parametric magnon transduction to spin qubits

Abstract

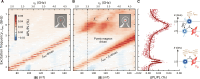
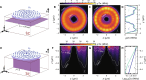
The integration of heterogeneous modular units for building large-scale quantum networks requires engineering mechanisms that allow suitable transduction of quantum information. Magnon-based transducers are especially attractive due to their wide range of interactions and rich nonlinear dynamics, but most of the work to date has focused on linear magnon transduction in the traditional system composed of yttrium iron garnet and diamond, two materials with difficult integrability into wafer-scale quantum circuits. In this work, we present a different approach by using wafer-compatible materials to engineer a hybrid transducer that exploits magnon nonlinearities in a magnetic microdisc to address quantum spin defects in silicon carbide. The resulting interaction scheme points to the unique transduction behavior that can be obtained when complementing quantum systems with nonlinear magnonics.

Fig. 1.. Parametric quantum transducer based on vortex magnons.

(A) Parametric generation of magnons via three-magnon splitting. The initial pump mode f₀ splits into secondary modes f₊ and f₋ following specific selection rules. (n, m) are the radial and azimuthal indices of the quantized vortex magnons. M_dyn denotes the dynamic component of the magnetization vector. (B) A permalloy (Py) disc with 5.1-μm diameter and 50-nm thickness on top of a SiC substrate hosting an ensemble of V_Si(V2) defects. An on-chip antenna surrounding the disc is used to excite the vortex magnons. (C) Crystallographic structure of the 4H SiC polytype showing the V_Si(V2) defect residing at the quasicubic lattice site. (D) General coupling principle. The ν_1,2 resonances of the V_Si(V2) cross the secondary magnon modes at two distinct field ranges (dashed circles) allowing pure-magnon addressability of the spin qubits. The observed branching of the secondary f₊ and f₋ modes with increasing out-of-plane field ∣B∣ corresponds to the exchange-induced splitting of the degenerate doublets as the vortex transitions into a vortex-cone state (29, 64). (E) Ground state energy level structure and optical transitions of V_Si(V2). Intersystem crossing (ISC) allows spin initialization and readout. At ∣B∣ ≠ 0, energy levels split due to Zeeman interaction. ZFS, zero-field splitting. The spatial profiles of the modes in (A) and their FFT (fast Fourier transform) spectra in (D) were obtained using micromagnetic simulations.

Fig. 2.. Optical detection of magnon-driven V_Si(V2) spin transitions.

(A) Reference ODMR spectra as a function of the external magnetic field ∣B∣ measured at the center of a microwave antenna without the vortex disc (see inset). The diagonal ΔPL/PL intensity corresponds to the field-dependent V_Si(V2) resonances. The discrete-like resonances are due to coarse increments in the applied magnetic field (see the Supplementary Materials). (B) ODMR spectra as a function of external magnetic field ∣B∣ for V_Si(V2) ensembles below the vortex disc (see inset). The off-diagonal signal around f_exc ∼ 6-GHz results from V_Si(V2) spin transitions purely driven by the parametric magnon modes f₋ and f₊. (C) ODMR spectrum at ∣B∣ = 90-mT, as extracted along the dashed line in (B). The energy diagram illustrates the origin of the two distinct features in the spectrum. g denotes the spin-magnon coupling strength. The spectra in (A) and (B) were both obtained by applying 9 dBm of microwave power. 3MS, three-magnon splitting.

Fig. 3.. Threshold process of the parametric driving scheme.

(A) ODMR spectra for increasing microwave excitation powers at ∣B∣ = 99-mT for V_Si(V2) below the disc (see inset). (B) ODMR contrast averaged over a 20-MHz-frequency window centered at f_exc= 6.24-GHz showing the characteristic threshold behavior of the three-magnon splitting. Three distinct microwave power ranges can be identified as follows: (I) below threshold, (II) above threshold, and (III) saturation. For each range, the average ODMR spectrum is shown in (C) and the corresponding average BLS spectrum is shown in (D). V_Si in (D) refers to ν₀. Solid line in (B) is a sigmoidal fit to the data.

Fig. 4.. Room-temperature coupling between the vortex magnons and the V_Si(V2) spins.

(A) Schematic depicting plane located 175-nm below the bottom surface of the disc, where the spin-magnon coupling strength is calculated. (B and C) Coupling strength g for the parametric modes f₋ and f₊ at ∣B∣ = 90-mT and ∣B∣ = 130-mT, respectively, at the plane shown in (A). (D) Coupling strength extracted along x = 0-μm from the intensity maps shown in (B) and (C). (E) Schematic depicting cross-sectional plane located at y = 0-μm starting 25-nm below the disc. (F and G) Coupling strength g for the parametric magnons f₋ and f₊ at ∣B∣ = 90-mT and ∣B∣ = 130-mT, respectively, at the plane shown in (E). (H) Coupling strength for the f₋ and f₊ modes along x = −1.05-μm and x = 0.6-μm as extracted from (F) and (G), respectively.